Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, tìm hình chiếu của: a) Tìm hình chiếu của SA trên các mặt phẳng (SBC) và (SCD) b) Tìm hình chiếu của SC trên các mp (SAB) (SAD) c) Tìm hình chiếu của AB trên mp (SCD)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
.png)
\(\begin{array}{l}\left. \begin{array}{l} + )BC \bot AB\left( {hcn\,\,ABCD} \right)\\BC \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\\AB \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAB} \right);AM \subset \left( {SAB} \right) \Rightarrow BC \bot AM\\\left. \begin{array}{l} + )CD \bot AD\left( {hcn\,\,ABCD} \right)\\CD \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\\AD \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow CD \bot \left( {SAD} \right);AN \subset \left( {SAD} \right) \Rightarrow CD \bot AN\end{array}\)
\(\begin{array}{l}\left. \begin{array}{l} + )AM \bot SB\\AM \bot BC\\SB \cap BC = \left\{ B \right\}\end{array} \right\} \Rightarrow AM \bot \left( {SBC} \right);SC \subset \left( {SBC} \right) \Rightarrow SC \bot AM\\\left. \begin{array}{l} + )AN \bot SD\\AN \bot CD\\SD \cap CD = \left\{ D \right\}\end{array} \right\} \Rightarrow AN \bot \left( {SCD} \right);SC \subset \left( {SCD} \right) \Rightarrow SC \bot AN\\\left. \begin{array}{l} + )AM \bot SC\\AN \bot SC\\AM \cap AN = \left\{ A \right\}\end{array} \right\} \Rightarrow SC \bot \left( {AMN} \right)\end{array}\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
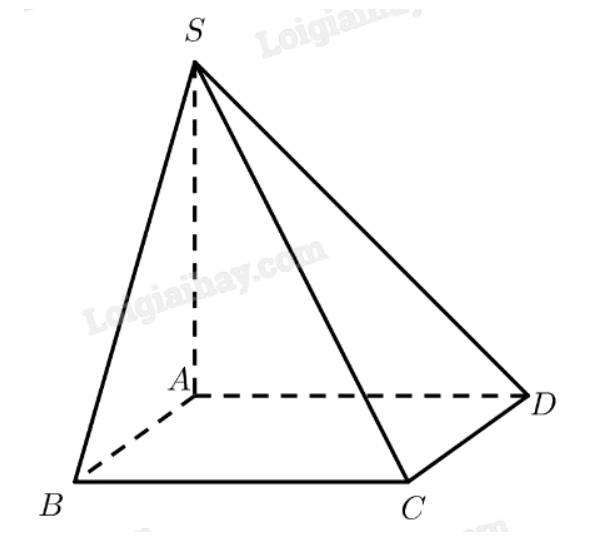
• Ta có:
\(\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BC\\AB \bot BC\end{array} \right\} \Rightarrow BC \bot \left( {SAB} \right)\)
Vậy \(B\) là hình chiếu vuông góc của điểm \(C\) trên mặt phẳng \(\left( {SAB} \right)\).
• Ta có:
\(\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot A{\rm{D}}\\AB \bot A{\rm{D}}\end{array} \right\} \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
Vậy \(A\) là hình chiếu vuông góc của điểm \(D\) trên mặt phẳng \(\left( {SAB} \right)\).
Lại có \(B\) là hình chiếu vuông góc của điểm \(C\) trên mặt phẳng \(\left( {SAB} \right)\).
Vậy đường thẳng \(AB\) là hình chiếu vuông góc của đường thẳng \(CD\) trên mặt phẳng \(\left( {SAB} \right)\).
• Ta có:
\(A\) là hình chiếu vuông góc của điểm \(D\) trên mặt phẳng \(\left( {SAB} \right)\).
\(B\) là hình chiếu vuông góc của điểm \(C\) trên mặt phẳng \(\left( {SAB} \right)\).
\(S \in \left( {SAB} \right)\)
Vậy tam giác \(SAB\) là hình chiếu vuông góc của tam giác \(SCD\) trên mặt phẳng \(\left( {SAB} \right)\).
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow\left(SCD\right)\perp\left(SAD\right)\)
\(AC=\sqrt{AD^2+CD^2}=a\sqrt{2}\)
\(BC=\sqrt{BE^2+CE^2}=a\sqrt{2}\)
\(\Rightarrow AC^2+BC^2=AB^2\Rightarrow AC\perp BC\)
\(\Rightarrow BC\perp\left(SAC\right)\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\)
b.
\(CD\perp\left(SAD\right)\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(\Rightarrow\widehat{SDA}=30^0\Rightarrow SA=AD.tan30^0=\dfrac{a\sqrt{3}}{3}\)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
Qua S kẻ đường thẳng d song song AD
Do \(AD||CE\) \(\Rightarrow\) d là giao tuyến (SAD) và (SCE)
Mà \(d\perp\left(SAB\right)\Rightarrow\widehat{ASE}\) là góc giữa (SAD) và (SCE)
\(AE=\dfrac{AB}{2}=a\)
\(tan\widehat{ASE}=\dfrac{AE}{SA}=\sqrt{3}\Rightarrow\widehat{ASE}=60^0\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
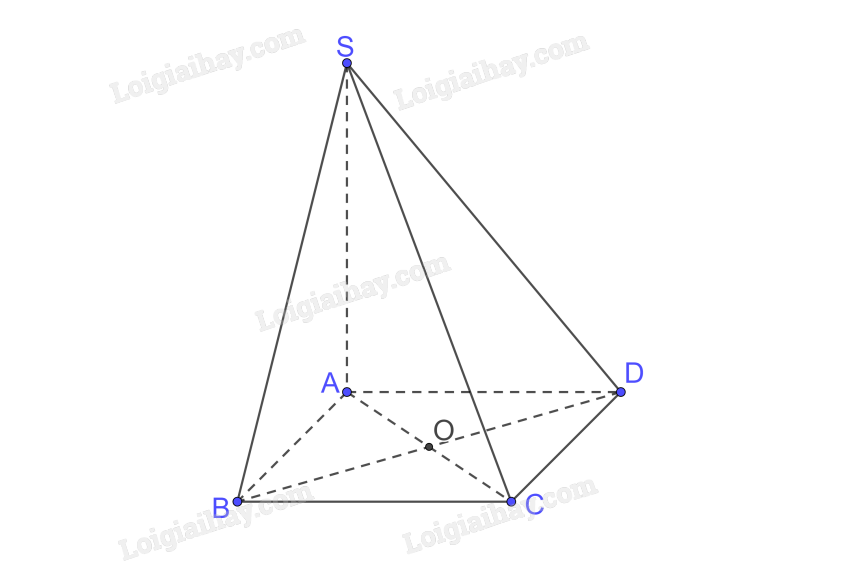
a) A là hình chiếu của S trên (ABCD) \(\left( {SA \bot \left( {ABCD} \right)} \right)\)
C là hình chiếu của C trên (ABCD)
\( \Rightarrow \) AC là hình chiếu của SC trên (ABCD)
\( \Rightarrow \) \(\left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
Xét tam giác ABC vuông tại B có
\(A{C^2} = A{B^2} + B{C^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \)
Xét tam giác SAC vuông tại A có
\(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{a\sqrt 2 }}{{a\sqrt 2 }} = 1 \Rightarrow \widehat {SCA} = {45^0}\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = {45^0}\)
b) \(\left. \begin{array}{l}AC \bot BD\left( {hv\,\,ABCD} \right)\\SA \bot BD\left( {SA \bot \left( {ABCD} \right)} \right)\\AC \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow \left( {BD,\left( {SAC} \right)} \right) = {90^0}\)
c) Gọi \(AC \cap BD = \left\{ O \right\}\) mà \(BD \bot \left( {SAC} \right)\)
\( \Rightarrow \) O là hình chiếu của B trên (SAC)
S là hình chiếu của S trên (SAC)
\( \Rightarrow \) SO là hình chiếu của SB trên (SAC).
CM
24 tháng 3 2019
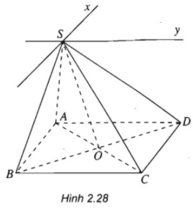
a)
Ta có:
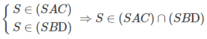
Giả sử:
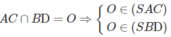
⇒ O ∈ (SAC) ∩ (SBD)
⇒ (SAC) ∩ (SBD) = SO
b) Ta có:
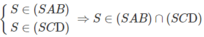
Ta lại có
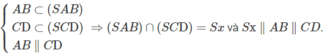
c) Lập luận tương tự câu b) ta có ⇒ (SAD) ∩ (SBC) = Sy và Sy // AD // BC.
6 tháng 9 2023
d: \(CD\subset\left(HKCD\right)\)
\(CD\subset\left(ABCD\right)\)
Do đó: \(\left(HKCD\right)\cap\left(ABCD\right)=CD\)
a: \(O\in BD\subset\left(SBD\right)\)
\(O\in AC\subset\left(SAC\right)\)
Do đó: \(O\in\left(SBD\right)\cap\left(SAC\right)\)
=>\(\left(SBD\right)\cap\left(SAC\right)=SO\)
b: AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó: (SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
c; AD//BC
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
Do đó: (SAD) giao (SBC)=mn, mn đi qua S và mn//AD//BC
a: AB vuông góc BC tại B
=>Hình chiếu của SA lên (SBC) là SB
AD vuông góc DC tại D
=>Hình chiếu của SA lên (SDC) là SD
b: CB vuông góc AB tại B
=>Hình chiếu của SC trên (SAB) là SB
CD vuông góc AD tại D
=>Hình chiếu của SC lên (SAD) là SD