mọi người cho mình hỏi có phải sin2a*cos2b - cos2a*sin2b chính là sin2(a-b) phải ko
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
0
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 6 2019
\(P=sin^22a+cos^22a+sin^22b+cos^22b+2sin2a.sin2b+2cos2a.cos2b\)
\(P=2+2\left(sin2a.sin2b+cos2a.cos2b\right)=2+2cos\left(2a-2b\right)\)
\(P=2+2cos\frac{\pi}{3}=3\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 5 2020
\(cos2A+cos2B+cos2C=2cos\left(A+B\right).cos\left(A-B\right)+2cos^2C-1\)
\(=-2cosC.cos\left(A-B\right)+2cos^2C-1\)
\(=-2cosC\left[cos\left(A-B\right)-cosC\right]-1\)
\(=-2cosC\left[cos\left(A-B\right)+cos\left(A+B\right)\right]-1\)
\(=-4cosC.cosA.cosB-1\)
\(sin2A+sin2B+sin2C=2sin\left(A+B\right)cos\left(A-B\right)+2sinC.cosC\)
\(=2sinC.cos\left(A-B\right)+2sinC.cosC\)
\(=2sinC\left[cos\left(A-B\right)+cosC\right]=2sinC\left[cos\left(A-B\right)-cos\left(A+B\right)\right]\)
\(=-4sinC.sinA.sin\left(-B\right)=4sinA.sinB.sinC\)
CM
14 tháng 11 2019
Chọn D.
Ta có: A = sin2(a + b) –sin2a - sin2b
= ( sina.cosb + cosa.sinb) 2 - sin2a - sin2b
= sin2a.cos2b + 2sina.cosb.cosa.sinb + cos2a.sin2b - sin 2a - sin2b
= sin2a( cos2b - 1) + sin2b( cos2a - 1) + 2.sina.cosa.sinb.cosb
= - sin2a.sin2b - sin2b.sin2a + 2.sina.cosa.sinb.cosb
= 2sina.sinb( cosa.cosb - sina.sinb) = 2.sina.sinb.cos( a + b).
CM
28 tháng 2 2017
Chọn A.
Sử dụng công thức hạ bậc và biến đổi tổng thành tích ta có :
A = sin2(a + b) – sin2a - sin2b
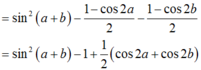
= -cos2(a + b) + cos( a + b) cos(a - b)
= cos (a +b) [ cos( a - b) – cos(a + b) ]
= 2 sina. sinb.cos(a + b)