Bài tập: Không dùng công thức nghiệm thu gọn, giải phương trình \(4mx^2-x-10m^2=0\) với x = 2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\Leftrightarrow\left(2m-4\right)^2-4\left(m^2-3\right)>=0\)
\(\Leftrightarrow4m^2-16m+16-4m^2+12>=0\)
=>-16m>=-28
hay m<=7/4
b: \(\Leftrightarrow16m^2-4\left(2m-1\right)\left(2m+3\right)=0\)
\(\Leftrightarrow16m^2-4\left(4m^2+4m-3\right)=0\)
=>4m-3=0
hay m=3/4
c: \(\Leftrightarrow\left(4m-2\right)^2-4\cdot4\cdot m^2< 0\)
=>-16m+4<0
hay m>1/4

a: =>(x-7)(x+3)=0
hay \(x\in\left\{7;-3\right\}\)
b: =>2x+7=0
hay x=-7/2
c: \(\Delta=50-4\cdot6\cdot2=50-48=2\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{5\sqrt{2}-\sqrt{2}}{12}=\dfrac{\sqrt{2}}{3}\\x_2=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)

7x2 - 6√2x + 2 = 0
a = 7; b' = -3√2; c = 2
Δ' =(b')2 - ac = (-3√2)2 - 7.2 = 4 ⇒ √(Δ') = 2
Phương trình có 2 nghiệm:
x1 = (3√2 + 2)/7; x2 = (3√2 - 2)/7

Phương trình bậc hai: ![]()
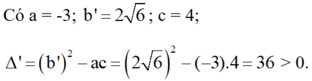
Phương trình có hai nghiệm phân biệt :
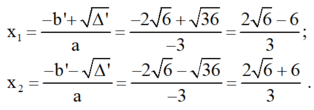

a) 3 x 2 + 8 x + 4 = 0 ;
a = 3; b' = 4; c = 4
Δ ' = ( b ' ) 2 - a c = 4 2 - 3 . 4 = 4 ⇒ √ ( Δ ' ) = 2
Phương trình có 2 nghiệm:
x 1 = ( - 4 + 2 ) / 3 = ( - 2 ) / 3 ; x 2 = ( - 4 - 2 ) / 3 = - 2
b) 7 x 2 - 6 √ 2 x + 2 = 0
a = 7; b' = -3√2; c = 2
Δ ' = ( b ' ) 2 - a c = ( - 3 √ 2 ) 2 - 7 . 2 = 4 ⇒ √ ( Δ ' ) = 2
Phương trình có 2 nghiệm:
x 1 = ( 3 √ 2 + 2 ) / 7 ; x 2 = ( 3 √ 2 - 2 ) / 7

1) \(4x^2-9=0\)
Theo pt ta có: \(a=4;b=0;c=-9\)
\(\Delta=b^2-4ac=0^2-4.4.\left(-9\right)=144>0\)
=> Pt có 2 nghiệm phân biệt
\(x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-0-\sqrt{144}}{2.4}=-\dfrac{3}{2}\\ x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-0+\sqrt{144}}{2.4}=\dfrac{3}{2}\)
2) \(-2x^2+50=0\)
Theo pt ta có: \(a=-2;b=0;c=50\)
\(\Delta b^2-4ac=0^2-4.\left(-2\right).50=400>0\)
=> PT có 2 nghiệm phân biệt
\(x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-0-\sqrt{400}}{2.\left(-2\right)}=5\\ x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-0+\sqrt{400}}{2a}=-5\)
3) \(3x^2+11=0\)
Theo pt ta có: \(a=3;b=0;c=11\)
\(\Delta=b^2-4ac=0^2-4.3.11=-132< 0\)
=> PT vô nghiệm

b; \(\text{Δ}=1^2-4\cdot\left(-2\right)\cdot\left(-3\right)=1-4\cdot6=-23< 0\)
Do đó: Phương trình vô nghiệm
c: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot11=1+44=45>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{1-3\sqrt{5}}{-2}=\dfrac{3\sqrt{5}-1}{2}\\x_2=\dfrac{-3\sqrt{5}-1}{2}\end{matrix}\right.\)
a, \(\Delta'=2-\left(-6\right)=8>0\)
vậy pt luôn có 2 nghiệm pb
\(x_1=-\sqrt{2}-2\sqrt{2};x_2=-\sqrt{2}+2\sqrt{2}\)
b, \(\Delta=1-4\left(-3\right)\left(-2\right)=1-16< 0\)
pt vô nghiệm
c, \(\Delta=1-4.11\left(-1\right)=1+44=45>0\)
pt luôn có 2 nghiệm pb
\(x_1=\dfrac{-1-3\sqrt{5}}{-2};x_2=\dfrac{-1+3\sqrt{5}}{-2}\)

a: \(2x^2-7x+3=0\)
=>\(2x^2-6x-x+3=0\)
=>\(2x\left(x-3\right)-\left(x-3\right)=0\)
=>(x-3)(2x-1)=0
=>\(\left[{}\begin{matrix}x-3=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{2}\end{matrix}\right.\)
b: \(6x^2+x+5=0\)
\(\text{Δ}=1^2-4\cdot6\cdot5=1-24\cdot5=1-120=-119< 0\)
=>Phương trình vô nghiệm
c: \(6x^2+x-5=0\)
=>\(6x^2+6x-5x-5=0\)
=>6x(x+1)-5(x+1)=0
=>(x+1)(6x-5)=0
=>\(\left[{}\begin{matrix}x+1=0\\6x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{5}{6}\end{matrix}\right.\)
d: \(3x^2+5x+2=0\)
=>\(3x^2+3x+2x+2=0\)
=>3x(x+1)+2(x+1)=0
=>(x+1)(3x+2)=0
=>\(\left[{}\begin{matrix}x+1=0\\3x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{2}{3}\end{matrix}\right.\)
e: \(y^2-8y+16=0\)
=>\(\left(y-4\right)^2=0\)
=>y-4=0
=>y=4
f: \(16z^2+24z+9=0\)
=>\(\left(4z\right)^2+2\cdot4z\cdot3+3^2=0\)
=>\(\left(4z+3\right)^2=0\)
=>4z+3=0
=>4z=-3
=>\(z=-\dfrac{3}{4}\)
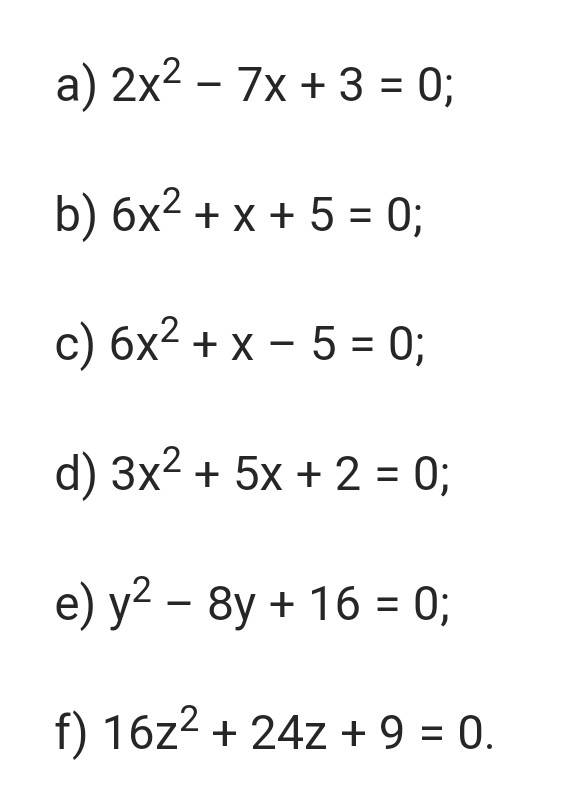 Chú ý b chẵn thì dùng công thức nghiệm thu gọn nhé
Chú ý b chẵn thì dùng công thức nghiệm thu gọn nhé
Thay \(x=2\) vào \(4mx^2-x-10m^2=0\)
\(\Rightarrow4m.2^2-2-10m^2=0\)
\(\Rightarrow16m-2-10m^2=0\)
\(\Rightarrow-10m^2+16m-2=0\)
\(\Rightarrow\left\{{}\begin{matrix}m_1=\dfrac{4+\sqrt{11}}{5}\\m_2=\dfrac{4-\sqrt{11}}{5}\end{matrix}\right.\)