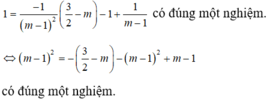Cho hàm số `y=x^3-3x+1` có đồ thị `(C)`.Tìm tất cả giá trị của a để qua điểm `A(a;-1)` kẻ 3 tiếp tuyến đến đồ thị `(C)` sao cho trong đó có 2 tiếp tuyến vuông góc với nhau.Ai giúp mình với ạ!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 2 2021
a, - Ta có : Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 6 .
\(\Rightarrow-\dfrac{b}{a}=-\dfrac{3}{a}=6\)
\(\Rightarrow a=-\dfrac{1}{2}\)
b, - Xét phương trình hoành độ giao điểm :\(3x+2=\left(2m-1\right)x+8\)
\(\Leftrightarrow3x+2=2mx-x+8\)
\(\Leftrightarrow3x+2-2mx+m-8=0\)
\(\Leftrightarrow x\left(3-2m\right)=6-m\)
- Để hai đường thẳng cắt được nhau thì : \(3-2m\ne0\)
\(\Leftrightarrow m\ne\dfrac{3}{2}\)
Vậy ...
9 tháng 2 2021
a) Vì đồ thị hàm số y=ax+3 cắt trục hoành tại điểm có hoành độ bằng 6 nên
Thay x=6 và y=0 vào hàm số y=ax+3, ta được:
\(6a+3=0\)
\(\Leftrightarrow6a=-3\)
hay \(a=-\dfrac{1}{2}\)
Vậy: \(a=-\dfrac{1}{2}\)
b)
Để hàm số y=(2m-1)x+8 là hàm số bậc nhất thì \(2m-1\ne0\)
\(\Leftrightarrow2m\ne1\)
hay \(m\ne\dfrac{1}{2}\)(1)
Để (d) cắt (d') thì \(2m-1\ne3\)
\(\Leftrightarrow2m\ne4\)
hay \(m\ne2\)(2)
Từ (1) và (2) suy ra \(m\notin\left\{\dfrac{1}{2};2\right\}\)
CM
16 tháng 3 2019
Đáp án B.
Pt tiếp tuyến đi qua A có dạng y=k(x-a)+1
Để có đúng 1 tiếp tuyến đi qua A thì hpt
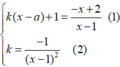
có đúng một nghiệm
Thay (2) vào (1):
CM
7 tháng 5 2017
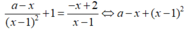
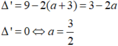
Đáp án B
Pt tiếp tuyến đi qua A có dạng y = k ( x − a ) + 1
Để có đúng 1 tiếp tuyến đi qua A thì hpt k ( x − a ) + 1 = − x + 2 x − 1 ( 1 ) k = − 1 ( x − 1 ) 2 ( 2 ) có đúng một nghiệm
Thay (2) vào (1):
CM
20 tháng 6 2017
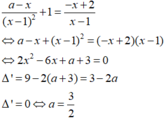
Gọi phương trình tiếp tuyến là y = k( x - a ) + 1. Xét hệ phương trình.
- x + 2 x - 1 = k x - a + 1 - 1 x - 1 2 = k ⇒ 2 x 2 - 6 x + a + 3 = 0 - 1 x - 1 2 ⇒ ∆ ' = 3 - 2 a
Để có 1 tiếp tuyến thì 2 x 2 - 6 x + a + 3 = 0 có 1 nghiệm kép khác 1 hoặc có 2 nghiệm trong đó 1 nghiệm bằng 1 có
TH1. có nghiệm kép ∆ = 0 ⇔ a = 3 2
TH2. Có nghiệm bằng 1 nên a = 1. Khi đó phương trình có 2 nghiệm x =1, x= 2
Vậy S = 3 2 ; 1
Đáp án cần chọn là C
CM
17 tháng 4 2019
+ Phương trình đường thẳng d đi qua A và có hệ số góc k là : y= k ( x-a) + 1
+ Phương trình hoành độ giao điểm của d và C :
Hay kx2+ (-k-ka+2) x-3+ka=0 ( *)
+ Với k= 0 , ta có d: y= 1 là tiệm cận ngang đồ thị hàm số nên không thể tiếp xúc được.
+ Với k≠0, d và C tiếp xúc nhau khi (1) có nghiệm kép
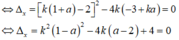
Coi đây là phương trình bậc 2 ẩn k tham số a
+ Để qua A( a; 1)vẽ được đúng tiếp tuyến thì phương trình ∆ =0 có đúng một nghiệm k≠0.
*Xét 1-a= 0 hay a=1, ta có 4k+4= 0 hay k= -1 thỏa mãn
*Có f( 0)=4 nên loại đi trường hợp có hai nghiệm trong đó có một nghiệm là 0.
*Còn lại là trường hợp ∆ x = 0 có nghiệm kép khi
Tổng là 1+ 3/2=5/2.
Chọn C.
BT
12 tháng 12 2017
a) Đề hàm số nghịch biến thì a - 3 < 0 \(\Leftrightarrow a< 3\).
b) Hàm số đi qua điểm M (1; -2 ) nên: \(\left(a-3\right).1-3=-2\)\(\Leftrightarrow a-3=1\)\(\Leftrightarrow a=4\).
c) Đồ thị hàm số là một đường thẳng song song với đường thẳng y = 3x nên \(a-3=3\Leftrightarrow a=6\).