Giải chi tiết giúp mình với! Mình để ảnh bài tập dưới phần bl ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
2
H
26 tháng 12 2022
Giải :
\(\dfrac{x+11}{89}+\dfrac{x+13}{87}-\dfrac{x+15}{85}-\dfrac{x+17}{83}=0\\ =>\left(\dfrac{x+11}{89}+1\right)+\left(\dfrac{x+13}{87}+1\right)-\left(\dfrac{x+15}{85}+1\right)-\left(\dfrac{x+17}{83}+1\right)=0\\ =>\left(\dfrac{x+11+89}{89}\right)+\dfrac{x+13+87}{87}-\dfrac{x+15+85}{85}-\dfrac{x+17+83}{83}=0\\ =>\dfrac{x+100}{89}+\dfrac{x+100}{87}-\dfrac{x+100}{85}-\dfrac{x+100}{83}=0\\ =>\left(x+100\right)\left(\dfrac{1}{89}+\dfrac{1}{87}-\dfrac{1}{85}-\dfrac{1}{83}\right)=0\\ =>\left[{}\begin{matrix}x+100=0\\\dfrac{1}{89}+\dfrac{1}{87}-\dfrac{1}{85}-\dfrac{1}{83}=0\left(voli\right)\end{matrix}\right.=>x=-100\)
NH
1
NH
2
H
26 tháng 12 2022
\(2x=3y\\ =>\dfrac{x}{3}=\dfrac{y}{2}\\ 4y=5z\\ =>\dfrac{y}{5}=\dfrac{z}{4}\\ \dfrac{x}{3}=\dfrac{y}{2}\\ =>\dfrac{x}{3.5}=\dfrac{y}{2.5}\\ =>\dfrac{x}{15}=\dfrac{y}{10}\\ \dfrac{y}{5}=\dfrac{z}{4}\\ =>\dfrac{y}{5.2}=\dfrac{z}{4.2}\\ =>\dfrac{y}{10}=\dfrac{z}{8}\\ =>\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{8}\)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{8}=\dfrac{x+y+z}{15+10+8}=\dfrac{11}{33}=\dfrac{1}{3}\\ =>\left\{{}\begin{matrix}x=\dfrac{1}{3}.15=5\\y=\dfrac{1}{3}.10=\dfrac{10}{3}\\z=\dfrac{1}{3}.8=\dfrac{8}{3}\end{matrix}\right.\)
NH
2
H
26 tháng 12 2022
Giải
\(\dfrac{x}{3}=\dfrac{y}{4}\\ \Leftrightarrow\dfrac{x}{3.3}=\dfrac{y}{4.3}\\\Leftrightarrow\dfrac{x}{9}=\dfrac{y}{12}\\ \dfrac{y}{3}=\dfrac{z}{5}\\ \Leftrightarrow \dfrac{y}{3.4}=\dfrac{z}{5.4}\\ \Leftrightarrow\dfrac{y}{12}=\dfrac{z}{20}\\ =>\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{20}\)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{20}=\dfrac{2x+3x+z}{2.9+3.12+20}=\dfrac{6}{74}=\dfrac{3}{37}\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{3}{37}\times9=\dfrac{27}{37}\\y=\dfrac{3}{37}\times12=\dfrac{36}{37}\\z=\dfrac{3}{37}\times20=\dfrac{60}{37}\end{matrix}\right.\)
NH
2
NH
2
H
26 tháng 12 2022
\(a,\dfrac{3^{10}.11+9^5.5}{27^3.2^4}.x=-9\\ =>\dfrac{3^{10}.11+\left(3^2\right)^5.5}{\left(3^3\right)^3.2^4}.x=-9\\ =>\dfrac{3^{10}.\left(11+5\right)}{3^9.2^4}.x=-9\\ =>\dfrac{3^{10}.16}{3^9.2^4}.x=-9\\ =>\dfrac{3^{10}.2^4}{3^9.2^4}.x=-9\\ =>3^1.x=-9\\ =>x=-9:3\\ =>x=-3\)
NH
2
H
26 tháng 12 2022
Giải
\(\sqrt{\dfrac{9}{4}}-\left|2x+1\right|=0,75\)
TH1: \(\left|2x+1\right|=2x+1\)
\(=>\sqrt{\dfrac{9}{4}}-\left(2x+1\right)=0,75\\ =>\dfrac{3}{2}-2x-1=\dfrac{3}{4}\\ =>\left(\dfrac{3}{2}-1\right)-2x=\dfrac{3}{4}\\ =>\dfrac{1}{2}-2x=\dfrac{3}{4}\\ =>2x=\dfrac{1}{2}-\dfrac{3}{4}\\ =>2x=-\dfrac{1}{4}\\ =>x=\left(-\dfrac{1}{4}\right):2\\ =>x=-\dfrac{1}{8}\)
\(TH2:\left|2x+1\right|=-2x-1\\ =>\sqrt{\dfrac{9}{4}}-\left(-2x-1\right)=\dfrac{3}{4}\\ =>\dfrac{3}{2}+2x+1=\dfrac{3}{4}\\ =>\left(\dfrac{3}{2}+1\right)+2x=\dfrac{3}{4}\\ =>\dfrac{5}{2}+2x=\dfrac{3}{4}\\ =>2x=\dfrac{3}{4}-\dfrac{5}{2}\\ =>2x=-\dfrac{7}{4}\\ =>x=\left(-\dfrac{7}{4}\right):2\\ =>x=-\dfrac{7}{8}\)
NH
2
H
26 tháng 12 2022
Giải
\(a,5-\left(x-2\right)^2=-4\\ =>\left(x-2\right)^2=5-\left(-4\right)\\ =>\left(x-2\right)^2=9\\ =>\left[{}\begin{matrix}\left(x-2\right)^2=3^2\\\left(x-2\right)^2=\left(-3\right)^2\end{matrix}\right.=>\left[{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.=>\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
Vậy \(x=5;x=-1\)
NH
2
H
26 tháng 12 2022
Giải
\(đk:6x-2\ne0=>x\ne\dfrac{1}{3}\\\dfrac{x+2}{6x-2}=\dfrac{1}{4}\\ =>\dfrac{4\left(x+2\right)}{4\left(6x-2\right)}=\dfrac{6x-2}{4\left(6x-2\right)}\\ =>4\left(x+2\right)=6x-2\\ =>4x+8-6x+2=0\\ =>-2x+10=0\\ =>-2x=-10\\ =>x=\left(-10\right):\left(-2\right)\\ =>x=5\left(thoamanđk\right)\)
Vậy \(x=5\)
NH
3
4 tháng 1 2023
cái câu này ngoài biện pháp tu từ nhân hóa ra mình chưa nhìn ra biện pháp nào cả có khi bạn phải xem lại:((
CC
Cô Châu Hạnh
Giáo viên
5 tháng 1 2023
Nhân hóa ở chỗ nhân vật xưng "ta" này là con vật (dựa vào câu nói "Dại gì ta phải theo ông chủ ra đồng"). Con vật nhưng có cách xưng hô, nói chuyện như một con người là nhân hóa nhé!
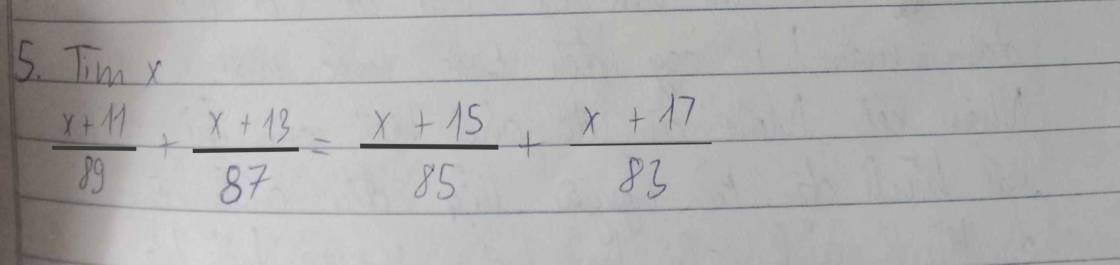
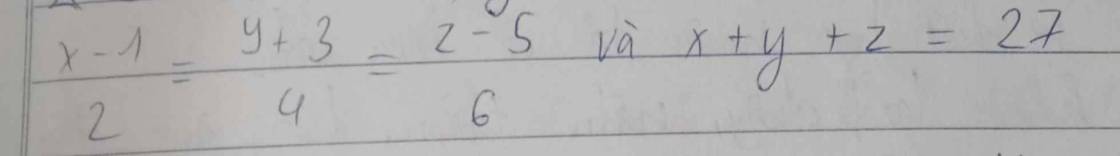
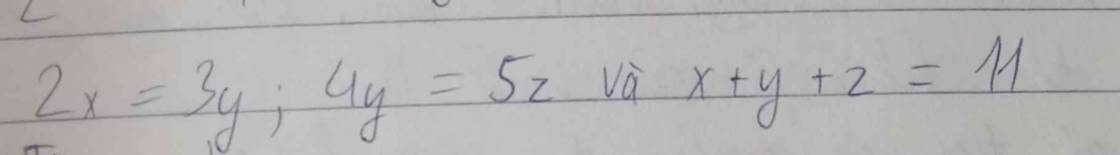
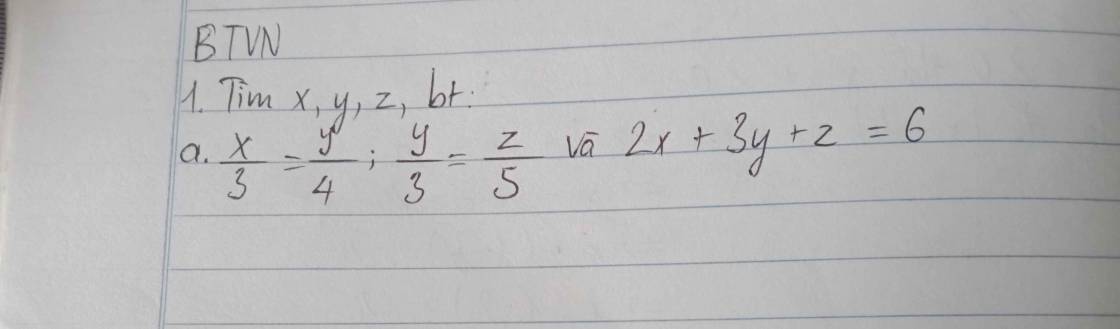
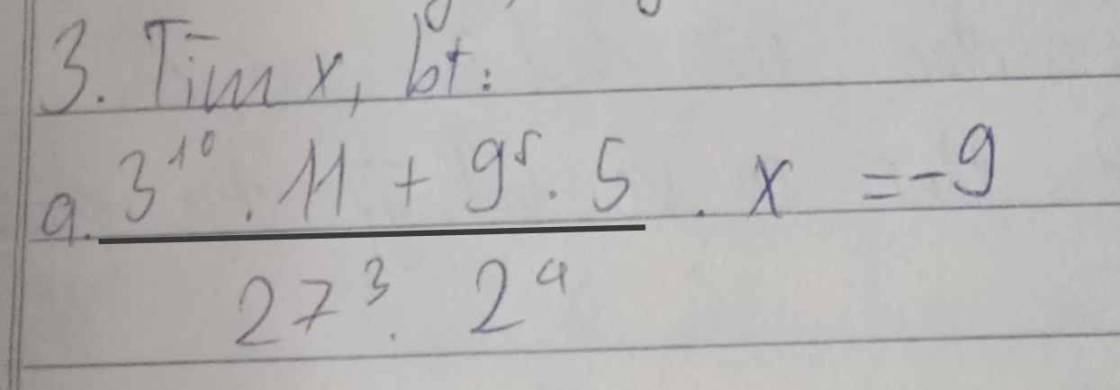
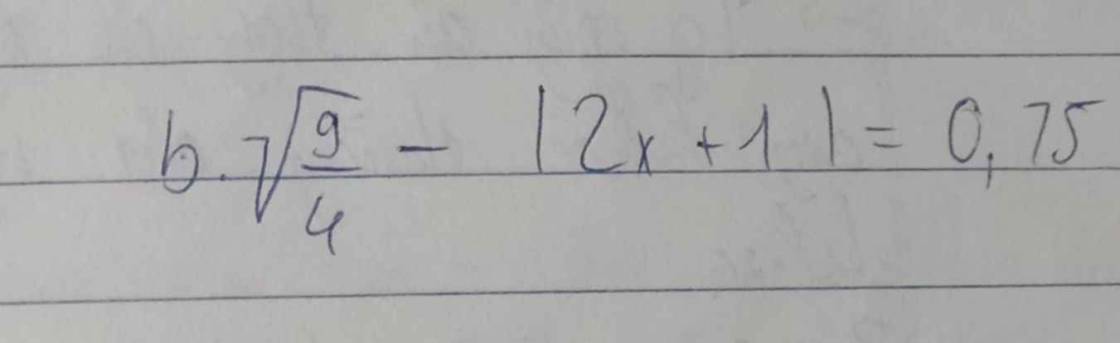
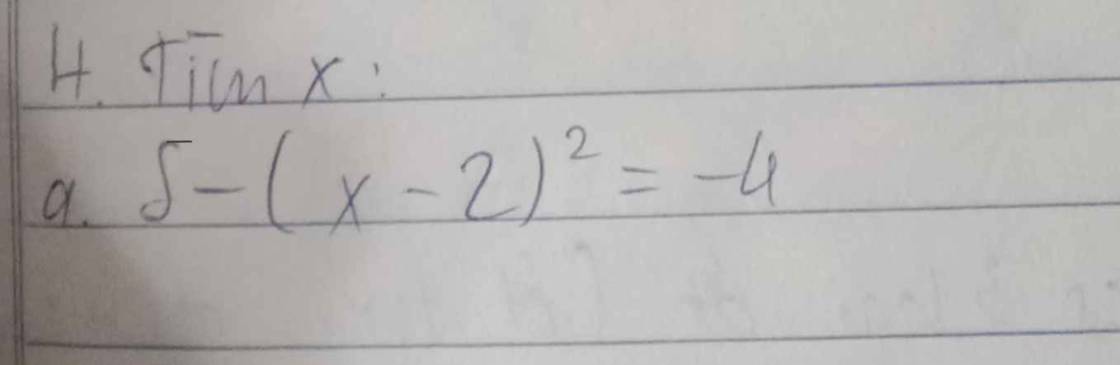
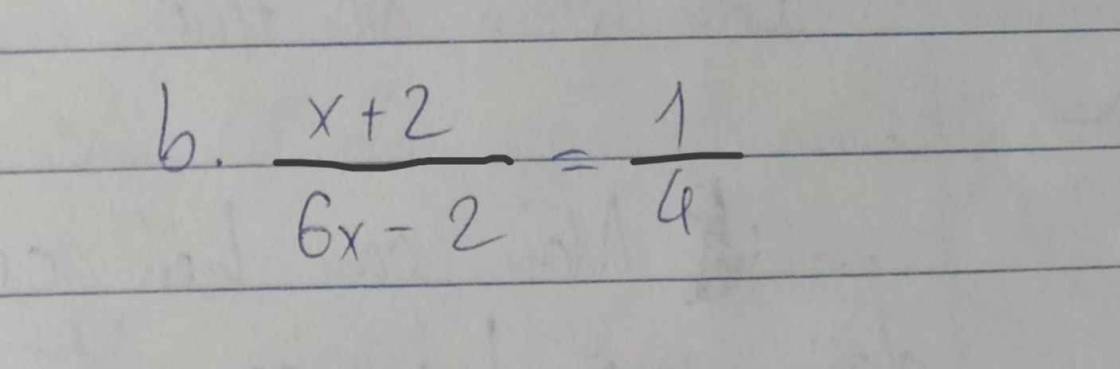
1. Look! The sun is setting behind the mountains
2. I have been waiting for half an hour but she didn't come
3. if she had enough money,I would choose english to learn
4. In the end, I decided not to buy that dictionary because it was too expensive
5. this video is so interesting that I have seen it twice