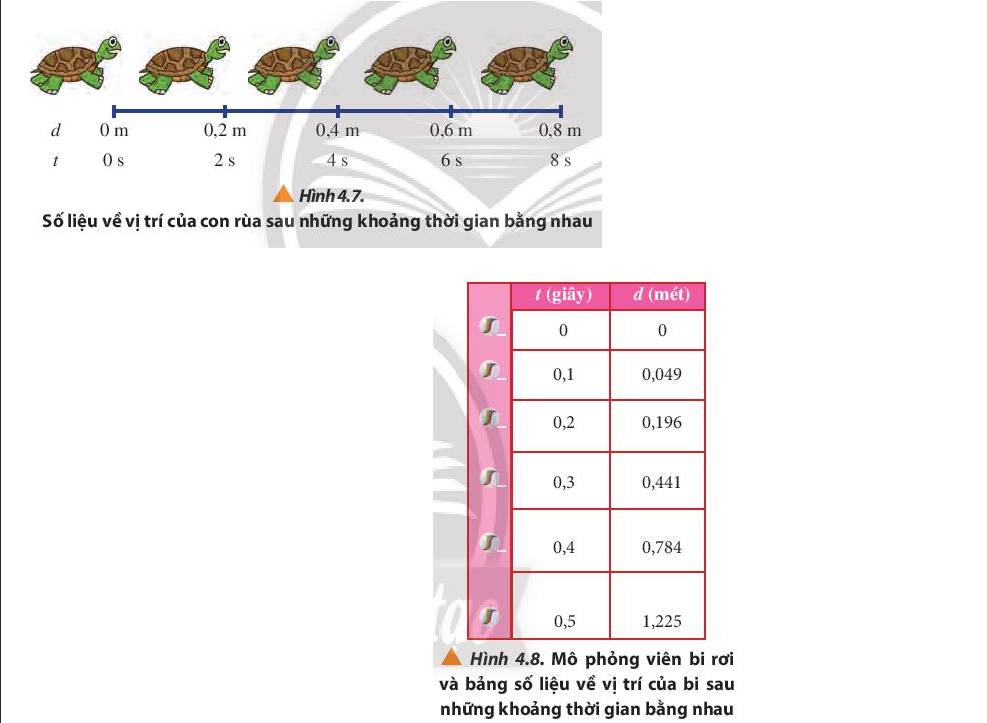
7. Dùng số liệu của hai chuyển động trong Hình 4.7 và 4.8:
a) Xác định độ dịch chuyển trong các khoảng thời gian liên tiếp bằng nhau của mỗi chuyển động.
b) Vẽ vào vở đồ thị dịch chuyển – thời gian (d – t) ứng với mỗi chuyển động
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
- Hình 4.7
\(\begin{array}{l}\Delta {d_1} = {x_2} - {x_1} = 0,5 - 0 = 0,5(m)\\\Delta {d_2} = {x_3} - {x_2} = 1,0 - 0,5 = 0,5(m)\\\Delta {d_3} = {x_4} - {x_3} = 1,5 - 1,0 = 0,5(m)\\\Delta {d_4} = {x_5} - {x_4} = 2,0 - 1,5 = 0,5(m)\end{array}\)
- Hình 4.8
\(\begin{array}{l}\Delta {d_1} = {x_2} - {x_1} = 0,049 - 0 = 0,049(m)\\\Delta {d_2} = {x_3} - {x_2} = 0,196 - 0,049 = 0,147(m)\\\Delta {d_3} = {x_4} - {x_3} = 0,441 - 0,196 = 0,245(m)\\\Delta {d_4} = {x_5} - {x_4} = 0,784 - 0,441 = 0,343(m)\\\Delta {d_5} = {x_6} - {x_5} = 1,225 - 0,784 = 0,441(m)\end{array}\)
b)
- Hình 4.7:
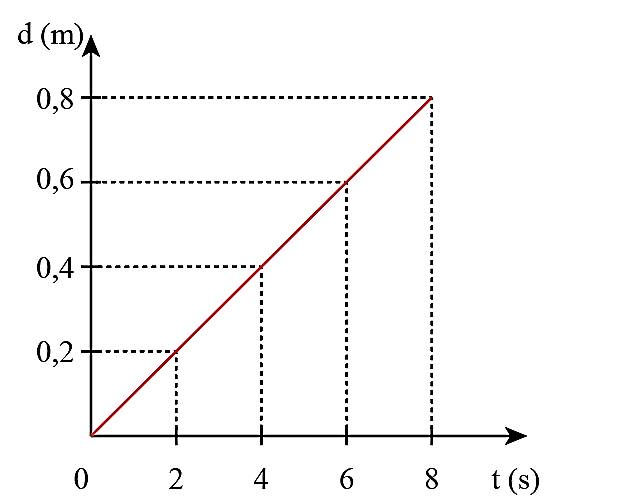
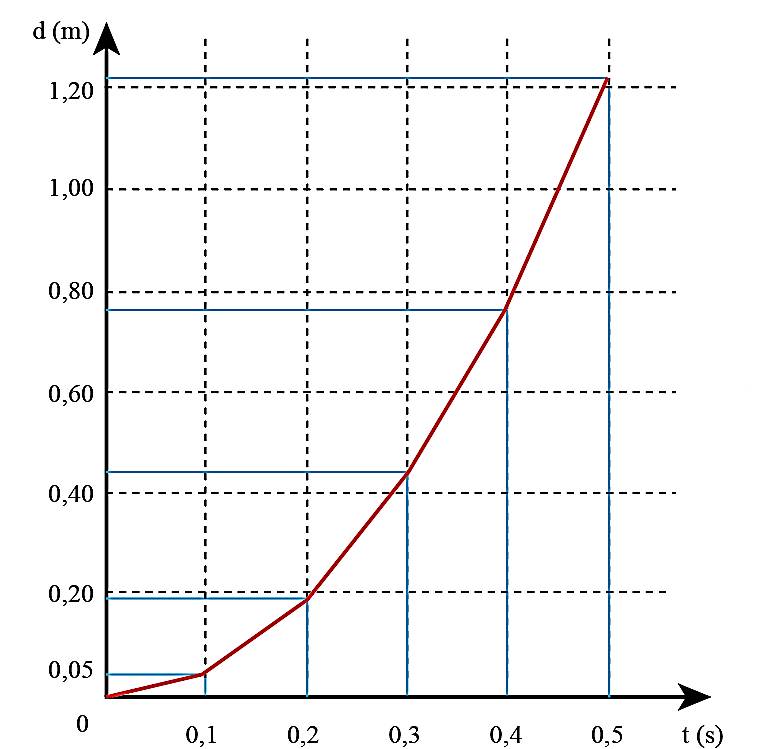
- Hình 4.8:

tọa độ ban đầu là -100m
tốc độ 2m/s
chuyển động theo chiều dương

a) Vẽ đồ thị:
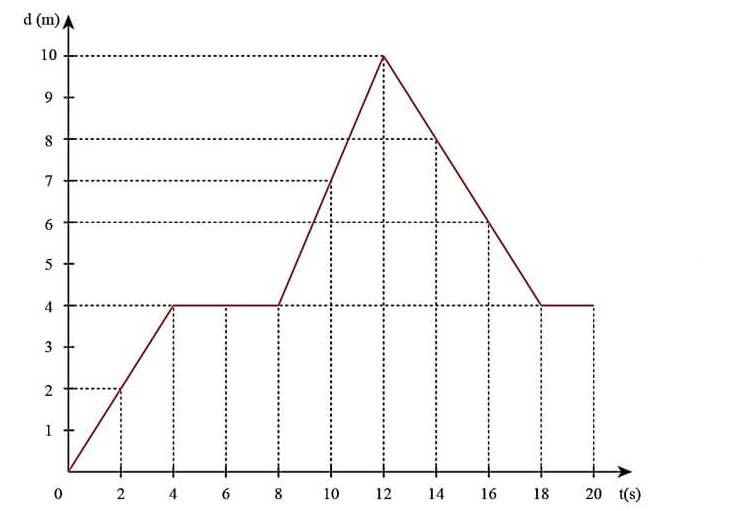
b)
- Vận tốc tức thời:
+ t = 2 s: \(v = \frac{d}{t} = \frac{2}{2} = 1(m/s)\)
+ t = 4 s: \(v = \frac{d}{t} = \frac{4}{4} = 1(m/s)\)
+ t = 6 s: \(v = \frac{d}{t} = \frac{4}{6} \approx 0,67(m/s)\)
+ t = 10 s: \(v = \frac{d}{t} = \frac{7}{{10}} = 0,7(m/s)\)
+ t = 16 s: \(v = \frac{d}{t} = \frac{6}{{16}} = 0,375(m/s)\)
- Tốc độ tức thời:
+ t = 2 s: \(v = \frac{s}{t} = \frac{2}{2} = 1(m/s)\)
+ t = 4 s: \(v = \frac{s}{t} = \frac{{2 + 4}}{4} = 1,5(m/s)\)
+ t = 6 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4}}{6} \approx 1,67(m/s)\)
+ t = 10 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4 + 4 + 7}}{{10}} = 2,1(m/s)\)
+ t = 16 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4 + 4 + 7 + 10 + 8 + 6}}{{16}} = 2,8125(m/s)\)

a) Vật 1 và vật 2 chuyển động cùng chiều và có vận tốc bằng nhau, vì đồ thị của chúng là hai đường thẳng song song nhau.
b) Phương trình chuyển động của các vật
Vật 1: x 1 = 4 t (m);
Vật 2: x 2 = 120 − 4 t (m);
Vật 3: x 3 = 40 + 4 t (m).
c) Vật 2 và vật 3 gặp nhau tại t = 10s, tọa độ x A = 80 m .

Chọn A.
*Chuyển động thẳng đều tọa độ biến thiên đều theo thời gian.