Trong các phương trình sau,phương trình nào có ít nhất một nghiệm là số nguyên?
A.\(\left(x-\sqrt{5}\right)^2=5\) B.9x2-1=0 C.4x2-4x+1=0 D.x2+x+2=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Phương trình 4 x 2 + 2 x − 5 = 0
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-et ta có: 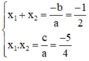
b) Phương trình . 9 x 2 − 12 x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ 2 = ( - 6 ) 2 - 4 . 9 = 0
⇒ Phương trình có nghiệm kép x 1 = x 2 .
Theo hệ thức Vi-et ta có: 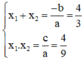
c) Phương trình 5 x 2 + x + 2 = 0
Có a = 5; b = 1; c = 2 ⇒ Δ = 1 2 − 4.2.5 = − 39 < 0
⇒ Phương trình vô nghiệm.
d) Phương trình 159 x 2 − 2 x − 1 = 0
Có a = 159; b = -2; c = -1; a.c < 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 .
Theo hệ thức Vi-et ta có: 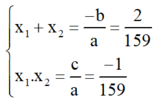

\(\Leftrightarrow x^2-4x+5+3\sqrt{x^2-4x+5}-2=0\)
Đặt \(\sqrt{x^2-4x+5}=t>0\)
\(\Rightarrow t^2+3t-2=0\Rightarrow\left[{}\begin{matrix}t=\dfrac{-3+\sqrt{17}}{2}\\t=\dfrac{-3-\sqrt{17}}{2}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x^2-4x+5=\dfrac{13-3\sqrt{17}}{2}\)
\(\Leftrightarrow x^2-4x+\dfrac{-3+3\sqrt{17}}{2}=0\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=4^2-2\left(\dfrac{-3+3\sqrt{17}}{2}\right)=19-3\sqrt{17}\)

a: =>(x-7)(x+3)=0
hay \(x\in\left\{7;-3\right\}\)
b: =>2x+7=0
hay x=-7/2
c: \(\Delta=50-4\cdot6\cdot2=50-48=2\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{5\sqrt{2}-\sqrt{2}}{12}=\dfrac{\sqrt{2}}{3}\\x_2=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)

a) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = 1,b = 2,c = - 20\)
Ta có \({a^2} + {b^2} - c = 1 + 4 + 20 = 25 > 0\). Vậy đây là phương trình đường tròn có tâm là \(I(1;2)\) và có bán kính \(R = \sqrt {25} = 5\)
b) Phương trình \({\left( {x + 5} \right)^2} + {\left( {y + 1} \right)^2} = 121\) là phương trình dường tròn với tâm \(I( - 5; - 1)\) và bán kinh \(R = \sqrt {121} = 11\)
c) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = - 3,b = - 2,c = - 2\)
Ta có \({a^2} + {b^2} - c = 9 + 4 + 2 = 15 > 0\). Vậy đây là phương trình đường tròn có tâm là \(I( - 3; - 2)\) và có bán kính \(R = \sqrt {15} \)
d) Phương trình không có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) nên phương trình đã cho không là phương trình đường tròn
Đáp án A.