Tam giác ABC có ABC=AC.M là trung điểm của BC a, AM là phân giác của góc BAC b, AM là đường trung trực của đoạn thẳng BC c, trên nửa mặt phẳng BC chứa A lấy điểm E sao cho EB=EC d, A, E, M thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TV
24 tháng 12 2020
さ→❖๖☆☆ I⃣K⃣K⃣I⃣ G⃣ấU⃣ A⃣N⃣I⃣M⃣E⃣❖༻꧂ •๖ۣۜTεαм ƒαʋσυɾĭтε αηĭмε⁀ᶦᵈᵒᶫ
LA
6 tháng 1 2018
Bài 1:
a) Xét tam giác ABM và tam giác ACM : AB=AC,AM chung ,BM=MC(vì M là trung điểm của BC gt)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.c.c\right)\)
b) Tam giác ABC có AB=AC nên tam giác ABC cân tại A
=> đường trung tuyến AM đồng thời là đường cao
Vậy AM vuông góc BC
c) Xét tam giác AEH và tam giác CEM : AE=EC,EH=EM,\(\widehat{AEH}=\widehat{CEM}\)(2 góc đối đỉnh)
\(\Rightarrow\Delta AEH=\Delta CEM\left(c.gc\right)\)
d) Ta có KB//AM(vì vuông góc với BM
\(\Rightarrow\widehat{KBD}=\widehat{DAM}\)(2 góc ở vị trí so le trong)
Xét tam giác KDB và MDA (2 góc đối đỉnh)
\(\Rightarrow\Delta KDB=\Delta DAM\left(g.c.g\right)\)
\(\Rightarrow KD=DM\left(1\right)\)
Tam giác ABM vuông tại M có trung tuyến MD
Nên : MD=BD=AD(2)
Từ (1) và (2) ta có : KD=DM=DB=AD
Tam giác KAM có trung tuyến ứng với cạnh KM là \(AD=\frac{AM}{2}\)
Nên : Tam giác KAM vuông tại A
Tương tự : Tam giác MAH vuông tại A
Ta có: Qua1 điểm A thuộc AM có 2 đường KA và AH cùng vuông góc với AM
Nên : K,A,H thẳng thàng
LA
6 tháng 1 2018
Bài 2 :
a) Ta có tam giác DAB=tam giác CEB(c.g.c)
Do : DA=CB(gt)
BE=BA(gt)
\(\widehat{DBA}=\widehat{CBE}\)(Cùng phụ \(\widehat{ABC}\))
=> DA=EC
b) Do tam giác DAB=tam giác CEB(ở câu a)
=> \(\widehat{BDA}=\widehat{BCE}\Rightarrow\widehat{BDA}+\widehat{BCD}=\widehat{BCE}+\widehat{BCD}\)
Mà : \(\widehat{BDA}+\widehat{BCD}=90^0\)( Do Bx vuông góc BC)
=> \(\widehat{BCE}+\widehat{BCD}=90^0\)
=> DA vuông góc với EC
CM
20 tháng 3 2019
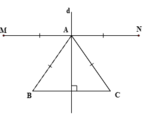
Ta có: B A M ^ = B ^ ( g t ) C A N ^ = C ^ ( g t )
Þ AM // BC; AN // BC (vì có cặp góc so le trong bằng nhau).
Þ 3 điểm M, A, N thẳng hàng (vì qua điểm A chỉ vẽ được một đường thẳng song song với BC).
Vậy MN // BC mà d ⊥ B C nên d ⊥ M N (1)
Ta có: A M = A B ; A N = A C
mà AB = AC (gt) nên AM = AN. (2)
Từ (1) và (2) Þ d là trung trực của MN
6 tháng 12 2016
Giải
a) vì m la trung diểm của BC => BM=MC
Xét tam giac BAM va tam giac MAC có:
AB=AC(dề bài cho)
BM=MC(Chung minh tren)
AM la cạnh chung(de bai cho)
=>Tam giác BAM=tam giac MAC(c.c.c)
b)từ trên
=>góc BAM=góc MAC(hai goc tuong ung)
Tia AM nam giua goc BAC (1)
goc BAM=goc MAC(2)
từ (1) va (2)
=>AM la tia phan giac cua goc BAC
c)Còn nữa ......-->
TT
7 tháng 8 2020
KHÔNG THẤY HÌNH THÌ VÀO THỐNG KÊ HỎI ĐÁP NHA
A) VÌ \(BH\perp AD\Rightarrow\widehat{BHA}=90^o\)
\(CI\perp AD\Rightarrow\widehat{CID}=90^o\)
\(\Rightarrow\widehat{BHA}=\widehat{CID}=90^o\)hay \(\widehat{BHI}=\widehat{CIH}=90^o\)
HAI GÓC NÀY Ở VỊ TRÍ SO LE TRONG BẰNG NHAU
=> BH // CI (ĐPCM)
B)
XÉT \(\Delta ABC\)VUÔNG TẠI A
\(\Rightarrow\widehat{A}=90^o\)hay \(\widehat{BAH}+\widehat{HAC}=90^o\left(1\right)\)
XÉT \(\Delta AHB\)VUÔNG TẠI H
\(\Rightarrow\widehat{H}=90^o\)hay \(\widehat{BAH}+\widehat{ABH}=180^o-90^o=90^o\left(2\right)\)
từ (1) và (2) \(\Rightarrow\widehat{HAC}=\widehat{ABH}\)
XÉT \(\Delta ABH\)VÀ\(\Delta CAI\)CÓ
\(\widehat{H}=\widehat{I}=90^o\)
AB = AC (gt)
\(\widehat{ABH}=\widehat{IAC}\)(CMT)
=>\(\Delta ABH\)=\(\Delta CAI\)(C-G-C)
=> BH = AI ( HAI CẠNH TƯƠNG ỨNG )
a: ΔABC cân tại A
mà AM là trung tuyến
nen AM là phân giác của góc BAC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM là trung trực của BC(1)
c: EB=EC
nên E nằm trên trung trực của BC(2)
Từ (1), (2) suy ra A,M,E thẳng hàng