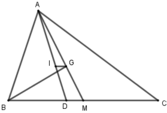
Cho tam giác ABC có AB + AC = 2BC. I là giao điểm các đường phân giác trong, G là trọng tâm. Chứng minh rằng:
a, Diện tích tam giác ABC gấp 3 lần diện tích tam giác BIC.
b, IG//BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 7 2017
1/. _Kẻ pg AD và đ/cao AE (D ; E thuộc BC) ta thấy AG/AE=2/3_bt:(1)
Trong tg ABC vớí pg AD ta có : DB/DC= AB/AC=6/12=1/2 <=> BD=3 ; DC=6 (cm)
Trong tg ABD với pg BI ta có : IA/IB=AB/BD =3/6 <=>AI/AD=2/3 -bt:(2). từ (1) & (2)suy ra đpcm
góc AED=^ACB=48 độ ( hai góc đều cọng với góc^BED thì =180 độ
CM
26 tháng 12 2019
Do M là trung điểm BC nên MB = 1 2 BC = 1 2 .15 = 7,5 cm
Mà BD = 6cm nên DM = 7,5 cm – 6cm = 1,5 cm
Do IG // DM nên I G D M = A G A M = 2 3 => IG = 2 3 DM = 1 3 .1,5 = 1 cm
Đáp án: A
a) Gọi IP, IQ, IS lần lượt là khoảng cách từ I đến BC, CA, AB => IP = IQ = IS
Ta có SABC = SBIC +SAIC +SAIB = 1/2.IP.BC +1/2.IQ.AC +1/2.IS.AB =1/2.IP(BC +CA +AB) = 1/2.IP.3BC( vì AB + AC = 2BC) = 3SBIC
b) Gọi D, M lần lượt là giao điểm của AI, AG với BC.
Trong tam giác ABC có AD là phân giác => \(\frac{AC}{DC}=\frac{AB}{DB}=\frac{AB+AC}{DC+DB}=\frac{AB+AC}{BC}=2\)2
Trong tam giác ABD có BI là phân giác => \(\frac{AI}{ID}=\frac{AB}{DB}=2\)
Mặt khác do G là trọng tâm tg ABC => \(\frac{AG}{GM}=2\)
=> \(\frac{AI}{ID}=\frac{AG}{GM}\)=> IG //BC (Talet đảo)