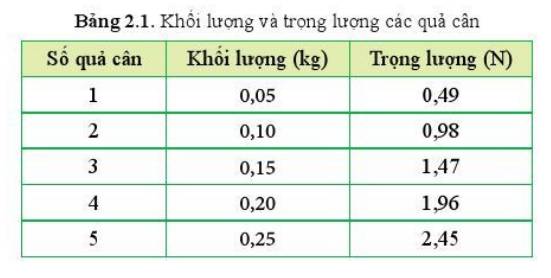
Từ bảng 2.1, xác định gia tốc rơi tự do ở vị trí thực hiện phép đo. Lấy kết quả đến 3 chữ số có nghĩa.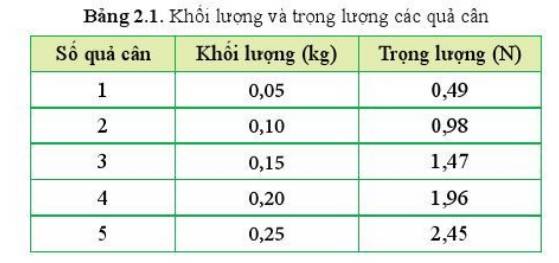
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 9 2023
Ta có: g = 1,6 m/s2
+ 1 quả cân: P = 0,05.1,6 = 0,08 (N)
+ 2 quả cân: P = 0,10.1,6 = 0,16 (N)
+ 3 quả cân: P = 0,15.1,6 = 0,24 (N)
+ 4 quả cân: P = 0,20. 1,6 = 0,32 (N)
+ 5 quả cân: P = 0,25.1,6 = 0,40 (N).
6 tháng 4 2022
Cơ năng vật ban đầu:
\(W=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}\cdot m\cdot40^2=800m\left(J\right)\)
Cơ năng tại vị trí thả vật:
\(W'=\dfrac{1}{2}mv'^2+mgz'=\dfrac{1}{2}\cdot m\cdot0^2+m\cdot10\cdot z'=m\cdot10\cdot z'\left(J\right)\)
Bảo toàn cơ năng: \(W=W'\)
\(\Rightarrow800m=m\cdot10\cdot z'\Rightarrow z'=80m\)
Vị trí thả vật cách đất một đoạn 80m.
6 tháng 4 2022
Áp dụng công thức v^2-v0^2=2as --> s= 80
Tức là độ cao 80m so với vị trí tiếp đất
21 tháng 11 2021
\(g=\overline{g}\pm\Delta g=9,78\pm0,44\)
Sai số tỉ đối:
\(\delta g=\dfrac{\Delta g}{\overline{g}}\cdot100\%=\dfrac{0,44}{9,78}\cdot100\%\approx4,5\%\)
Sử dụng công thức tính trọng lực: \(P=m . g\)
Ta có:
Thí nghiệm thả quả cân được thực hiện ở cùng một vị trí (vì khối lượng, trọng lượng của một quả cân là như nhau) vì vậy trong các lần đo khi thay đổi khối lượng các quả cân sẽ là như nhau.
Gia tốc rơi tự do của một quả cân khi treo là:
\(g_1=\dfrac{P_1}{m_1}=\dfrac{0,49}{0,05}=9,8\) (m/s2)
=> Gia tốc rơi tự do ở vị trí khi thức hiện phép đo là: 9,80 m/s2 (làm tròn đến 3 chữ số có nghĩa)