cho chóp SABCD đáy hình bình hành M là trung điểm SC , mặt anpha chứa AM cắt SD,SB tại E;F tính SD/SE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để tính thể tích SAPMQ, ta cần tìm độ dài đoạn PM và đoạn MQ. Gọi E là trung điểm của BD. Ta có ME song song với AM và ME = 1/2 BD = 1/2 a. Vì (∆) song song với BD nên góc AME = góc ABD = 45 độ. Vì SA vuông góc với ABCD nên góc SAM = 90 độ. Vì SA = a√3 và góc SAM = 90 độ nên tam giác SAM là tam giác vuông cân tại A. Do đó, góc ASM = 45 độ. Vì góc ASM = góc AME = 45 độ nên tam giác ASM và tam giác AME đồng dạng. Vậy, ta có: AM/AS = AE/AM AM^2 = AS * AE AM^2 = (a√3) * (1/2 a) AM^2 = a^2 * √3 / 2 AM = a√3 / √2 AM = a√6 / 2 Ta có ME = 1/2 a Vậy, PM = AM - ME = (a√6 / 2) - (1/2 a) = (a√6 - a) / 2 Tương tự, ta có MQ = AM + ME = (a√6 / 2) + (1/2 a) = (a√6 + a) / 2 Vậy, thể tích SAPMQ = SABC * PM = a^2 * (a√6 - a) / 2 = a^3√6 / 2 - a^3 / 2

Trong tam giác SBD, MN là đường trung bình \(\Rightarrow MN||BD\)
\(\Rightarrow MN||\left(ABCD\right)\)
Trong mp (ABCD), qua E kẻ đường thẳng song song BD cắt BC tại F và cắt AD kéo dài tại G
Trong mp (SAD), nối GN kéo dài cắt SA tại P
Ngũ giác PNEFM là thiết diện của (MNE) và chóp

Gọi O là tâm đáy và I là trung điểm MN
\(\Rightarrow\) I cũng là trung điểm SO (định lý Talet)
Trong tam giác SAC, nối AI cắt SC tại E
Áp dụng định lý Menelaus:
\(\dfrac{SE}{EC}.\dfrac{CA}{AO}.\dfrac{OI}{SI}=1\Leftrightarrow\dfrac{SE}{EC}.2.1=1\Rightarrow SE=\dfrac{1}{2}EC\)
\(\Rightarrow SE=\dfrac{1}{3}SC\)
Do chóp đều \(\Rightarrow\left\{{}\begin{matrix}V_{SAMEN}=2V_{SANE}\\V_{SABCD}=2V_{SACD}\end{matrix}\right.\)
\(\Rightarrow\dfrac{V_{SAMEN}}{V_{SABCD}}=\dfrac{V_{SANE}}{V_{SACD}}=\dfrac{SA}{SA}.\dfrac{SN}{SD}.\dfrac{SE}{SC}=1.\dfrac{1}{2}.\dfrac{1}{3}=\dfrac{1}{6}\) (định lý Simsons)

Chọn A
Xét một trường hợp đặc biệt của các điểm M, E, F ta tính được T = 1.
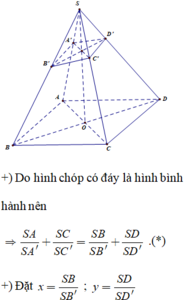
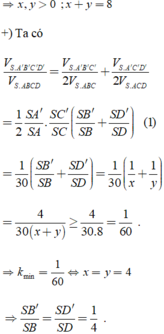

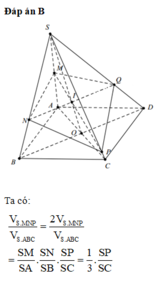

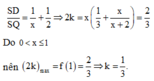
Đề thiếu dữ liệu rồi em, mp \(\left(\alpha\right)\) chỉ có tính chất chứa AM thì ko thể tính được tỉ số SD/SE (có vô số giá trị thỏa mãn)