cho tam giác ABC. gọi D là trung điểm của BC. NỐi A tới D, E là trung điểm của AD. Nối B đến E kéo dài cắt AC tại G. Nối E đến C
a, Tìm tất cả cấc tam giác có diện tích bằng \(\frac{1}{4}\)diện tích ABC.
b, So sánh AG và GC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ MK vuông góc AC
\(S_{AME}=\dfrac{1}{2}\cdot MK\cdot AE\)
\(S_{MEC}=\dfrac{1}{2}\cdot MK\cdot EC\)
mà AE=1/4*EC
nên \(S_{AME}=\dfrac{1}{4}\cdot S_{MEC}\)
=>\(S_{MEC}=80\left(cm^2\right)\)

Giải
Ta có: S ABC = S CBD (vì có cùng chiều cao hạ từ đỉnh B xuống đáy AC)
S ABC (S CBD) là:
360 : 2 = 180 (cm\(^2\))
Ta có: S BAE = S CAE (vì có cùng chiều cao hạ từ đỉnh A xuống đáy BC)
S BAE (S CAE) là:
360 : 2 = 180 (cm\(^2\))
Ta có: S ABI = S EBI (vì có cùng chiều cao hạ từ đỉnh B xuống đáy AE)
S ABI (S EBI) là:
180 : 2 = 90 (cm\(^2\))
Ta có: S ABI = S AID = 90 cm\(^2\) (vì có cùng chiều cao hạ từ đỉnh A xuống đáy BD)
Vậy diện tích của tam giác AID là 90 cm\(^2\)

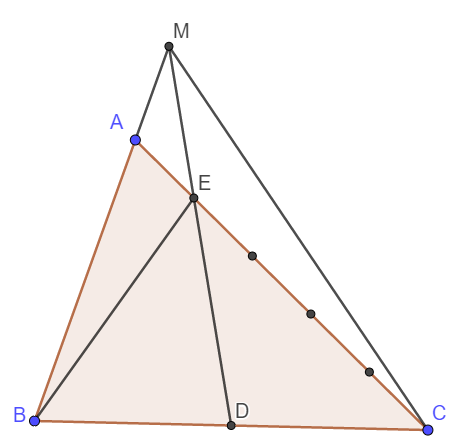
a) Ta thấy ngay tam giác MAE và tam giác MEC có chung chiều cao hạ từ M xuống AC, EC = 4AE nên \(S_{MEC}=4S_{MAE}=4\times20=80\left(cm^2\right)\)
b) Ta thấy tam giác MBD và tam giác MCD có chung chiều cao và đáy BD = DC nên \(S_{MBD}=S_{MCD}\)
Ta thấy tam giác EBD và tam giác ECD có chung chiều cao và đáy BD = DC nên \(S_{EBD}=S_{ECD}\)
Vậy nên \(S_{MBE}=S_{MEC}=80\left(cm^2\right)\)
Ta có \(\frac{S_{AME}}{S_{MEC}}=\frac{1}{4};\frac{S_{ABE}}{S_{EBC}}=\frac{1}{4}\Rightarrow\frac{S_{AME}+S_{ABE}}{S_{MEC}+S_{EBC}}=\frac{1}{4}\Rightarrow\frac{S_{MBE}}{S_{MEBC}}=\frac{1}{4}\)
\(\Rightarrow S_{MEBC}=4.80=320\left(cm^2\right)\)
\(\Rightarrow S_{MBC}=320+80=400\left(cm^2\right)\)
\(\Rightarrow S_{ABC}=400-20-80=300\left(cm^2\right)\)
a) D là trung điểm của BC nên CD = DB; E là trung điểm của AD nên AE = ED
S(ABD) = S(ADC) vì có đáy CD = DB và chung đường cao tương ứng với đáy
=> S(ABD) = S(ADC) = 1/2 S(ABC)
S(ABE) = S(EBD) vì có đáy AE = ED và có chung đường cao tương ứng với đáy
=> S(ABD) = S(EBC) = 1/2 S(ABD) = 1/4 S(ABC)
Tương tự trên
=> S(AEC) = S(EDC = 1/2 S(ADC) = 1/4 S(ABC)
Vậy : S(ABD) = S(EBC) = S(AEC) = S(EDC) = 1/4 S(ABC)
b) Nhìn hình ta thấy
AG = 1/2 GC