cho đường trong (O;3CM) và A là một điểm cố định thuộc đường tròn tại A . Trên d lấy điểm M ( M khác A) . Kẻ dây cung AB vuông góc với OM tại H
a) Tính độ dài OM và AB khi OH bằng 2cm
b) Chứng minh MB là tiếp tuyến của đường tròn (O)
c) Tìm vị trí của điểm M trên d sao cho diện tích tam giác HOA lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
10 tháng 12 2018
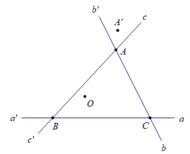
a. Giả sử ba đường thẳng aa’, bb’ và cc’ cắt nhau từng đôi một tại ba điểm A, B, C (hình vẽ). Điểm O cần vẽ là giao điểm của hai tia AO và BO sao cho tia AO nằm giữa hai tia AB và AC, tia BO nằm giữa hai tia BA và BC.
b. Điểm A’ nằm trên tia AA’ sao cho tia AA’ nằm giữa hai tia Ab’ và Ac, A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng BC.

CM
25 tháng 9 2018

Tam giác AO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên ![]()
Suy ra: CA ⊥ O’A tại điểm A
Vậy CA là tiếp tuyến của đường tròn (O’)
Tam giác BO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên ![]()
Suy ra: CB ⊥ O’B tại điểm B
Vậy CB là tiếp tuyến của đường tròn (O’)






a: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
OA^2=OH*OM
=>OM=9/2=4,5cm
\(HA=\sqrt{3^2-2^2}=\sqrt{5}\left(cm\right)\)
=>\(AB=2\sqrt{5}\left(cm\right)\)
b: Xét ΔOAM và ΔOBM có
OA=OB
góc AOM=góc BOM
OM chung
Do đó: ΔOAM=ΔOBM
=>góc OBM=90 độ
=>MB là tiếp tuyến của (O)