K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 7 2017
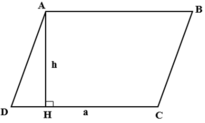
SABCD = AH.CD = 4.3 = 12(cm2)
Vì M là trung điểm của AB nên AM = 1 2 AB = 1 2 .4 = 2(cm)
Ta có chiều cao từ đỉnh D đến cạnh AM của tam giác ADM bằng chiều cao AH của hình bình hành.
=> SADM = 1 2 AH.AM = 1 2 .3.2 = 3(cm2)
Đáp án cần chọn là: A
DD
Đoàn Đức Hà
Giáo viên
12 tháng 9 2021
Chu vi hình bình hành ABCD là:
\(\left(12+8\right)\times2=40\left(cm\right)\)
Diện tích hình bình hành ABCD là:
\(12\times6=72\left(cm^2\right)\)
11 tháng 12 2021
Giải
Chu vi hình bình hành ABCD đó là :
\(\left(12+8\right)\times2=40\) ( cm )
Diện tích hình bình hành ABCD đó là :
\(12\times6=72\)( cm2 )
Đáp số : Chu vi : \(40\)cm ; Diện tích : \(72\)cm2
12 tháng 7 2023
a: Xét tứ giác AMCN có
AM//NC
AM=CN
=>AMCN là hình bình hành
b:
AM+MB=AB
CN+ND=CD
mà AM=CN và AB=CD
nên MB=ND
Xét tứ giác DMBN có
BM//DN
BM=DN
=>DMBN là hình bình hành
LT
2
SI
11 tháng 3 2021
Chu vi của hình bình hành ABCD là :
(8 + 6) x 2 = 28 (dm)
Đ/S : 28 dm
W
2 tháng 3 2020
a) Vì ABCD là hình bình hành nên AB=CD=25cm.
=>AM=BM=25:2=12,5(cm)(1)
S hình thang AMCD là:
\(\frac{\left(25+12,5\right)\cdot12}{2}=225\left(cm^2\right)\)
b)Vì AH và BH cùng là chiều cao nên AH=BH=12cm
Từ (1), suy ra S hình tam giác MBC là:
\(\frac{12,5\cdot12}{2}=75\left(cm^2\right)\)
đ/s
29 tháng 7 2021
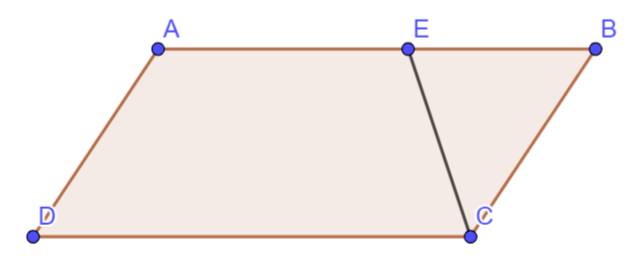
Ta có: \(AB=\dfrac{1}{2}CD\)(gt)
mà \(ED=EC=\dfrac{CD}{2}\)(E là trung điểm của CD)
nên AB=ED=EC
Xét tứ giác ABED có
AB//DE
AB=DE(cmt)
Do đó: ABED là hình bình hành
Xét tứ giác ABCE có
AB//CE
AB=CE
Do đó: ABCE là hình bình hành
D
29 tháng 7 2021
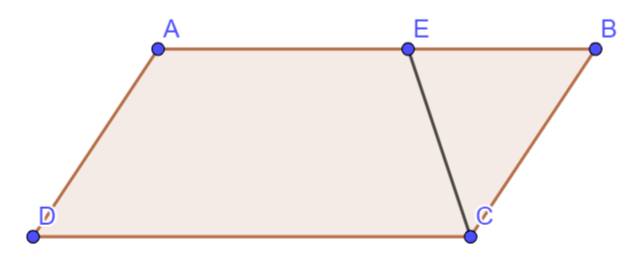
- Do E là trung điểm của CD
\(=>DE=CE=\dfrac{CD}{2}\)
Mà \(AB=\dfrac{1}{2}CD\) (gt)
\(=>AB=DE=CD\)
- DE và CE trùng CD, AB // CD => AB // DE // CE
Tứ giác ABED có:
- AB=DE (cmt)
- AB // DE (cmt)
Vậy: Tứ giác ABED là hình bình hành (đpcm)
- Tương tự: Tứ giác ABCE có
- AB=CE (cmt)
- AB // CE (cmt)
Vậy tứ giác ABCE là hình bình hành (đpcm)
CM
30 tháng 11 2019
Ta có : S = a.h
Khi đó ta có: S = 4.2 = 8 c m 2 .
Chọn đáp án B.