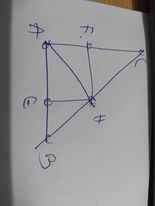
Cho tam giác ABC vuông tại A đường cao AH, M là hình chiếu của H lên AB, N là hình chiếu của H lên AC
a) So sánh HB và HC
b) So sánh NA và NC
c) So sánh MA và MB
d) So sánh AM và AN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 12 2023
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>AH=EF
b: Ta có: ΔABH vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2=6^2-3,6^2=23,04\)
=>\(HA=\sqrt{23,04}=4,8\left(cm\right)\)
Xét ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\)
=>\(AE\cdot6=4,8^2=23,04\)
=>\(AE=\dfrac{23.04}{6}=3,84\left(cm\right)\)
AEHF là hình chữ nhật
=>AE=HF
mà AE=3,84cm
nên HF=3,84cm
AH
Akai Haruma
Giáo viên
20 tháng 12 2023
Lời giải:
a/ Tứ giác $AEHF$ có 3 góc vuông: $\widehat{A}=\widehat{E}=\widehat{F}=90^0$ nên là hình chữ nhật.
$\Rightarrow AH=EF$
b/ $HF=AE$ (do $AEHF$ là hcn)
Xét tam giác $AEH$ và $AHB$ có:
$\widehat{A}$ chung
$\widehat{AEH}=\widehat{AHB}=90^0$
$\Rightarrow \triangle AEH\sim \triangle AHB$ (g.g)
$\Rightarrow \frac{AE}{AH}=\frac{AH}{AB}$
$\Rightarrow AE=\frac{AH^2}{AB}=\frac{AB^2-BH^2}{AB}=\frac{6^2-3,6^2}{6}=3,84$ (cm)
6 tháng 2 2022
2: Xét tứ giác AKHI có
\(\widehat{AKH}+\widehat{AIH}=180^0\)
Do đó: AKHI là tứ giác nội tiếp
Suy ra: \(\widehat{AIK}=\widehat{AHK}\)
mà \(\widehat{AHK}=\widehat{C}\)
nên \(\widehat{AIK}=\widehat{ACB}\)
3: Xét ΔAIK và ΔACB có
\(\widehat{AIK}=\widehat{ACB}\)
\(\widehat{KAI}\) chung
Do đó: ΔAIK∼ΔACB
18 tháng 11 2023
a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
=>AMHN là hình chữ nhật
=>AH=MN
b: Sửa đề: MH=MD
Xét ΔAHD có
AM là đường cao
AM là đường trung tuyến
Do đó: ΔAHD cân tại A
=>AH=AD
ΔAHD cân tại A
mà AB là đường cao
nên AB là phân giác của \(\widehat{HAD}\)
=>\(\widehat{HAD}=2\cdot\widehat{HAB}\)
Xét ΔAHE có
AC là đường cao(AC\(\perp\)EH)
AC là đường trung tuyến ứng với cạnh HE(N là trung điểm của HE, AC cắt HE tại N)
Do đó: ΔAHE cân tại A
=>AH=AE
ΔAHE cân tại A
mà AC là đường trung tuyến
nên AC là phân giác của \(\widehat{EAH}\)
=>\(\widehat{EAH}=2\cdot\widehat{HAC}\)
\(\widehat{EAD}=\widehat{EAH}+\widehat{DAH}\)
\(=2\left(\widehat{HAB}+\widehat{HAC}\right)=2\cdot90^0=180^0\)
=>E,A,D thẳng hàng
Xét ΔAHB và ΔADB có
AH=AD
\(\widehat{HAB}=\widehat{DAB}\)
AB chung
Do đó: ΔAHB=ΔADB
=>\(\widehat{AHB}=\widehat{ADB}=90^0\)
=>BD\(\perp\)DE(1)
Xét ΔAHC và ΔAEC có
AH=AE
\(\widehat{HAC}=\widehat{EAC}\)
AC chung
Do đó: ΔAHC=ΔAEC
=>\(\widehat{AHC}=\widehat{AEC}=90^0\)
=>CE\(\perp\)ED(2)
Từ (1),(2) suy ra BD//CE
Xét tứ giác BDEC có BD//EC
nên BDEC là hình thang
c: NF=HM
HM=NA
Do đó: NF=NA
=>N là trung điểm của AF
Xét tứ giác EFHA có
N là trung điểm chung của EH và FA
nên EFHA là hình bình hành
Hình bình hành EFHA có EH\(\perp\)FA
nên EFHA là hình thoi
16 tháng 3 2023
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>HB=HC
c: Xet ΔABC có
H là trung điểm của BC
HD//AC
=>D là trung điểm của AB
ΔAHB vuông tại H
mà HD là trung tuyến
nên HD=AB/2
d: CD<(CA+CB)/2
=>2CD<CA+CB
=>CD<DH+HC(luôn đúng)
17 tháng 5 2020
a) Tứ giác AIHK có góc H=K=I=A=90độ
=> AIHK LÀ HÌNH CHỮ NHẬT ( tỨ GIÁC CÓ 3 GÓC VUÔNG)
FG
26 tháng 10 2017
hình này nhìn đúng hơn đấy bạn và mình giải đây
a. ta có: AMH = 900 (M là hình chiếu vuông góc [do chỗ này đề sai nên mình sửa lại] của H lên AB)
ANH = 900 (N là hình chiếu vuông góc của H lên AC)
MAN = 900 (tam giác ABC vuông A)
=> tg (tứ giác) MHNA là hcn (hình chữ nhật)
=> AH = MN (trong hcn có tính chất của htc [hình thang cân] và htc có tính chất 2 đc (đường chéo) bằng nhau)
còn b với c thì mình chưa biết làm :v
Bài này xét từng cặp tam giác thôi.
a) Xét \(\Delta ABH\)và \(\Delta ACH\)có:
\(AH\): chung
\(\widehat{AHB}=\widehat{AHC}=90\)độ
\(\widehat{ABH}=\widehat{ACH}\)( cùng phụ \(\widehat{BAC}\))
\(\Rightarrow\Delta ABH=\Delta ACH\left(g.c.g\right)\)
\(\Rightarrow HB=HC\)(hai cạnh t.ứng)
Mấy câu sau bạn làm nốt. Gợi ý xét:
b) \(\Delta AHN\)và \(\Delta CHN\)
c) \(\Delta MBH\)và \(\Delta MAH\)
d) Câu này có 2 cách: chứng minh hình chữ nhật => chiều dài > chiều rộng hay cũng cm hình chữ nhật => song song => cặp góc bằng nhau ở vị trí so le trong hoặc đồng vị => xét bình thường như các câu kia.
Tuy nhiên nên chọn cách 2 vì cách 1 chiều dài > chiều rộng đôi khi không đúng thế. Vì có thể chiều dài nhỏ hơn hoặc bằng chiều rộng
Nếu cm cách 2 thì làm như sau:
Xét tứ giác \(AMHN\)có: \(\hept{\begin{cases}\widehat{HMA}=90\\MAN=90\\HNA=90\end{cases}}\)(gt)
\(\Rightarrow AMHN\)là hình chữ nhật
\(\Rightarrow MH\)// \(AN\)
\(\Rightarrow\widehat{MHA}=\widehat{HAN}\left(slt\right)\)
Sau đó xét \(\Delta MHA\)và \(\Delta HAN\)nhé.
Ps: Nhớ check lại.
AH vuông góc vs BC mà