Cho (O,R ) dây CD kẻ Ok vuông góc với CD cắt tiếp tuyến tại C của đường tròn tại điểm M
a, Vẽ hình chính xác
b, Chứng minh MD là tiếp tuyến
c Biết R= 10, CD= 16 tính OM
giúp mình với ạ mình cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: ΔOCD cân tại O
mà OM là đường cao
nên OM là phân giác của góc COD
Xét ΔOCM và ΔODM có
OC=OD
góc COM=góc DOM
OM chung
Do đó: ΔOCM=ΔODM
=>góc ODM=90 độ
=>MD là tiếp tuyến của (O)
c: KD=CD/2=8
OK=căn 10^2-8^2=6
OK*OM=OD^2
=>OM=10^2/6=100/6=50/3

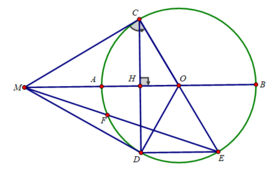
a) Xét tam giác COD cân tại O có OH là đường cao
⇒ OH cũng là tia phân giác ⇒ ∠(COM) = ∠(MOD)
Xét ΔMCO và ΔMOD có:
CO = OD
∠(COM) = ∠(MOD)
MO là cạnh chung
⇒ ΔMCO = ΔMOD (c.g.c)
⇒ ∠(MCO) = ∠(MDO)
∠(MCO) = 90 0 nên ∠(MDO) = 90 0
⇒ MD là tiếp tuyến của (O)

a: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC
b: Xét (O) có
ΔCND nội tiếp
CD là đường kính
Do đó: ΔCND vuông tại N
=>CN\(\perp\)ND tại N
=>CN\(\perp\)AD tại N
Xét ΔDCA vuông tại C có CN là đường cao
nên \(AN\cdot AD=AC^2\left(3\right)\)
Ta có: OA là trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOCA vuông tại C có CH là đường cao
nên \(AH\cdot AO=AC^2\left(4\right)\)
Từ (3) và (4) suy ra \(AN\cdot AD=AH\cdot AO\)
c: Ta có: \(AH\cdot AO=AN\cdot AD\)
=>\(\dfrac{AH}{AD}=\dfrac{AN}{AO}\)
Xét ΔAHN và ΔADO có
\(\dfrac{AH}{AD}=\dfrac{AN}{AO}\)
\(\widehat{HAN}\) chung
Do đó: ΔAHN đồng dạng với ΔADO
=>\(\widehat{AHN}=\widehat{ADO}\)
Ta có: ΔOCA vuông tại C
=>\(CO^2+CA^2=OA^2\)
=>\(CA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(CA=R\sqrt{3}\)
Ta có: ΔDCA vuông tại C
=>\(DC^2+CA^2=DA^2\)
=>\(DA^2=\left(2R\right)^2+\left(R\sqrt{3}\right)^2=7R^2\)
=>\(DA=R\sqrt{7}\)
Xét ΔDCA vuông tại C có \(sinCDA=\dfrac{CA}{DA}\)
=>\(sinCDA=\dfrac{R\sqrt{3}}{R\sqrt{7}}=\sqrt{\dfrac{3}{7}}=\dfrac{\sqrt{21}}{7}\)
=>\(sinAHN=\dfrac{\sqrt{21}}{7}\)

a: Xét (O) có
KB là tiếp tuyến
KC là tiếp tuyến
Do đó: KB=KC
hay K nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OK là đường trung trực của BC

b: ΔOCD cân tại O
mà OM là đường cao
nên OM là phân giác của góc COD
Xét ΔOCM và ΔODM có
OC=OD
góc COM=góc DOM
OM chung
Do đó: ΔOCM=ΔODM
=>góc ODM=90 độ
=>MD là tiếp tuyến của (O)
c: KD=CD/2=8
OK=căn 10^2-8^2=6
OK*OM=OD^2
=>OM=10^2/6=100/6=50/3
mình cảm ơn