cho tam giác DEF cân tại D có DF=DE=5,EF=8.M,N lần lượt là trung điểm DF,DE.Kẻ DH vuông góc với EF.Tính DH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 4 2023
a: Xet ΔDME và ΔDNF có
DM=DN
góc MDE chung
DE=DF
=>ΔDME=ΔDNF
=>EM=FN và góc DEM=góc DFN
b: Xet ΔNEF và ΔMFE có
NE=MF
EF chung
NF=ME
=>ΔNEF=ΔMFE
=>góc KEF=góc KFE
=>KE=KF
c: ΔDEF cân tại D
mà DH là đường cao
nên DH là trung tuyến
Xét ΔDEF có
DH,FN,EM là trung tuyến
=>DH,FN,EM đồng quy
8 tháng 4 2021
a) Ta có: \(DN=\dfrac{DE}{2}\)(N là trung điểm của DE)
\(DM=\dfrac{DF}{2}\)(M là trung điểm của DF)
mà DE=DF(ΔDEF cân tại D)
nên DN=DM
Xét ΔDNH vuông tại H và ΔDMH vuông tại M có
DN=DM(cmt)
DH chung
Do đó: ΔDNH=ΔDMH(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{NDH}=\widehat{MDH}\)(hai góc tương ứng)
hay \(\widehat{EDH}=\widehat{FDH}\)
Xét ΔEDH và ΔFDH có
DE=DF(ΔDEF cân tại D)
\(\widehat{EDH}=\widehat{FDH}\)(cmt)
DH chung
Do đó: ΔEDH=ΔFDH(c-g-c)
Suy ra: HE=HF(Hai cạnh tương ứng)
21 tháng 3 2022
a, Ta có: DH là đường cao trong tam giác cân DEF
⇒DH vừa là đường cao, vừa là đường trung tuyến trong tam giác cân DEF
⇒HE=HF
Ta có: HE=HF=EF/2=8/2=4 (cm)
Xét ΔDHE vuông tại H
Theo định lý Pi-ta-go, ta có:
DF²=DH²+HF²
⇒DH²=DF²-HF²
⇒DH²=5²-4²
⇒DH²=9
⇒DH=√9=3 (cm)
b, Xét ΔDME và ΔDNF có:
DM=DN (GT)
A là góc chung
DE=DF (GT)
⇒ ΔDME=ΔDNF (c.g.c)
⇒EM=FN (2 cạnh tương ứng)
DEM=DFN (2 góc tương ứng)
c, Ta có: E=F (GT)
và DEM=DFN (cmt)
⇒KEF=KFE
⇒ΔKEF cân tại K
⇒KE=KF
d, Ta có: DH⊥EF và HE=HF
⇒DH là đường trung trực của EF
mà KE=KF
⇒K là điểm thuộc đường trung trực DH
⇒D, K, H thẳng hàng
2 tháng 3 2022
a: Ta có: ΔDEF cân tại D
mà DH là đường cao
nên H là trung điểm của FE
hay HF=HE
b: EF=6cm nên HF=3cm
=>DH=4cm
c: Xét ΔDME và ΔDNF có
DM=DN
\(\widehat{EMD}\) chung
DE=DF
Do đó: ΔDME=ΔDNF
14 tháng 2 2022
a: Ta có: ΔDEF cân tại D
mà DH là đường cao
nên H là trung điểm của EF
hay EH=FH
b: EH=FH=EF/2=3(cm)
Xét ΔDHE vuông tại H có \(DE^2=DH^2+HE^2\)
nên DH=4(cm)
c: Xét ΔDEM và ΔDFN có
DE=DF
\(\widehat{EDM}\) chung
DM=DN
Do đó: ΔDEM=ΔDFN
Suy ra: \(\widehat{DEM}=\widehat{DFN}\)
d: Xét ΔNEH và ΔMFH có
NE=MF
\(\widehat{E}=\widehat{F}\)
EH=FH
Do đó: ΔNEH=ΔMFH
Suy ra: HN=HM
hay H nằm trên đường trung trực của MN(1)
Ta có: KM=KN
nên K nằm trên đường trung trực của MN(2)
Ta có: DN=DM
nên D nằm trên đường trung trực của MN(3)
Từ (1), (2) và (3) suy ra D,H,K thẳng hàng
14 tháng 2 2022
a. xét tam giác DHE và tam giác DHF, có:
D: góc chung
DE = DF ( DEF cân )
DH: cạnh chung
Vậy tam giác DHE = tam giác DHF ( c.g.c )
=> HE = HF ( 2 cạnh tương ứng )
b.ta có: EH = EF :2 ( EF là đường cao cũng là trung tuyến ) = 6 : 2 =3 cm
áp dụng định lý pitago vào tam giác vuông DHE, có:
\(DE^2=DH^2+EH^2\)
\(\Rightarrow DH=\sqrt{DE^2-EH^2}=\sqrt{5^2-3^2}=\sqrt{16}=4cm\)
c.xét tam giác DEM và tam giác DFN có:
DE = DF ( DEF cân )
DM = DN ( gt )
D: góc chung
Vậy tam giác DEM = tam giác DFN ( c.g.c )
=> góc DEM = góc DFN ( 2 góc tương ứng )
d.xét tam giác DKM và tam giác DKN, có:
DM = DN ( gt )
D: góc chung
DK: cạnh chung
Vậy tam giác DKM = tam giác DKN ( c.g.c )
=> góc DKM = góc DKN = 90 độ ( tam giác BNM cân, K là trung điểm cũng là đường cao )
=> DK vuông BC
Mà DH cũng vuông BC
=> D,H,K thẳng hàng
Chúc bạn học tốt!!!
25 tháng 1
Sửa đề; DH vuông góc EF tại H
a: Xét ΔDHE vuông tại H và ΔDHF vuông tại H có
DE=DF
DH chung
Do đó: ΔDHE=ΔDHF
=>HE=HF
b: Ta có: HE=HF
H nằm giữa E và F
Do đó: H là trung điểm của EF
=>\(HE=HF=\dfrac{EF}{2}=4\left(cm\right)\)
ΔDHE vuông tại H
=>\(DH^2+HE^2=DE^2\)
=>\(DH^2=5^2-4^2=9\)
=>\(DH=\sqrt{9}=3\left(cm\right)\)
c: Ta có: \(DM=MF=\dfrac{DF}{2}\)
\(DN=NE=\dfrac{DE}{2}\)
mà DF=DE
nên DM=MF=DN=NE
Xét ΔDME và ΔDNF có
DM=DN
\(\widehat{MDE}\) chung
DE=DF
Do đó: ΔDME=ΔDNF
=>EM=FN và \(\widehat{DEM}=\widehat{DFN}\)
d: Xét ΔNEF và ΔMFE có
NE=MF
NF=ME
EF chung
Do đó: ΔNEF=ΔMFE
=>\(\widehat{NFE}=\widehat{MEF}\)
=>\(\widehat{KEF}=\widehat{KFE}\)
=>ΔKEF cân tại K
8 tháng 4 2021
A) XÉT ΔDHE VÀ ΔDHF, CÓ
DE=DF (ΔDEF CÂN TẠI D)
\(\widehat{E}=\widehat{F}\) (ΔDEF CÂN TẠI D)
⇒ ΔDHE = ΔDHF (C.HUYỀN-G.NHỌN)
⇒\(\widehat{EDH}=\widehat{FDH}\) (2 GÓC T.ỨNG)
8 tháng 4 2021
TA CÓ : EN=\(\dfrac{1}{2}\)DE
MÀ : DE=DF
⇒EN=FM B) XÉT ΔNEF VÀ ΔMFE CÓ
EF: CHUNG
\(\widehat{E}=\widehat{F}\)( TAM GIÁC DEF CÂN TẠI D)
EN=FM (CMT)
⇒ΔNEF = ΔMFE (C-G-C)
⇒EM=FN (2 CẠNH TƯƠNG ỨNG)
C) TA CÓ : EH=FH (ΔDHE=ΔDHF)
MÀ : EF=8
⇒DH LÀ TRUNG ĐIỂM CỦA EF
⇒EH=\(\dfrac{1}{2}EF\) = \(\dfrac{1}{2}\) .8 = 4
⇒EH=4
TRONG ΔDHE VUÔNG TẠI H
\(DE^2=HE^2+DH^2\) (ĐỊNH LÝ PTG)
⇒\(5^2=4^2+DH^2\)
⇒\(DH^2\)=25-16
⇒\(DH^2\) = 9
⇒DH=\(\sqrt{9}\)=3
24 tháng 11 2023
a:
\(\widehat{HDE}+\widehat{E}=90^0\)(ΔHDE vuông tại H)
\(\widehat{E}+\widehat{F}=90^0\)(ΔEDF vuông tại D)
Do đó: \(\widehat{HDE}=\widehat{F}\)
ΔDEF vuông tại D
mà DM là đường trung tuyến
nên MD=MF
=>\(\widehat{MDF}=\widehat{MFD}=\widehat{F}\)
\(\widehat{EDH}+\widehat{MDH}+\widehat{FDM}=\widehat{EDF}=90^0\)
=>\(\widehat{F}+\widehat{MDH}+\widehat{F}=90^0\)
=>\(\widehat{MDH}+2\cdot\widehat{F}=\widehat{E}+\widehat{F}\)
=>\(\widehat{MDH}=\widehat{E}+\widehat{F}-2\cdot\widehat{F}=\widehat{E}-\widehat{F}\)
b:
Xét ΔDEF vuông tại D có DH là đường cao
nên \(DE\cdot DF=DH\cdot EF\)
ΔDEF vuông tại D
=>\(DE^2+DF^2=EF^2\)
\(\left(EF+DH\right)^2=EF^2+2\cdot EF\cdot DH+DH^2\)
\(=EF^2+2\cdot DE\cdot DF+DH^2\)
\(\left(DF+DE\right)^2=DF^2+2\cdot DF\cdot DE+DE^2\)
\(=\left(DF^2+DE^2\right)+2\cdot DF\cdot DE\)
\(=EF^2+2\cdot DH\cdot EF\)
\(\left(EF+DH\right)^2-\left(DF+DE\right)^2\)
\(=EF^2+2\cdot DH\cdot EF+DH^2-EF^2-2\cdot DH\cdot EF\)
\(=DH^2>0\)
=>EF+DH>DF+DE
=>EF-DE>DF-DH
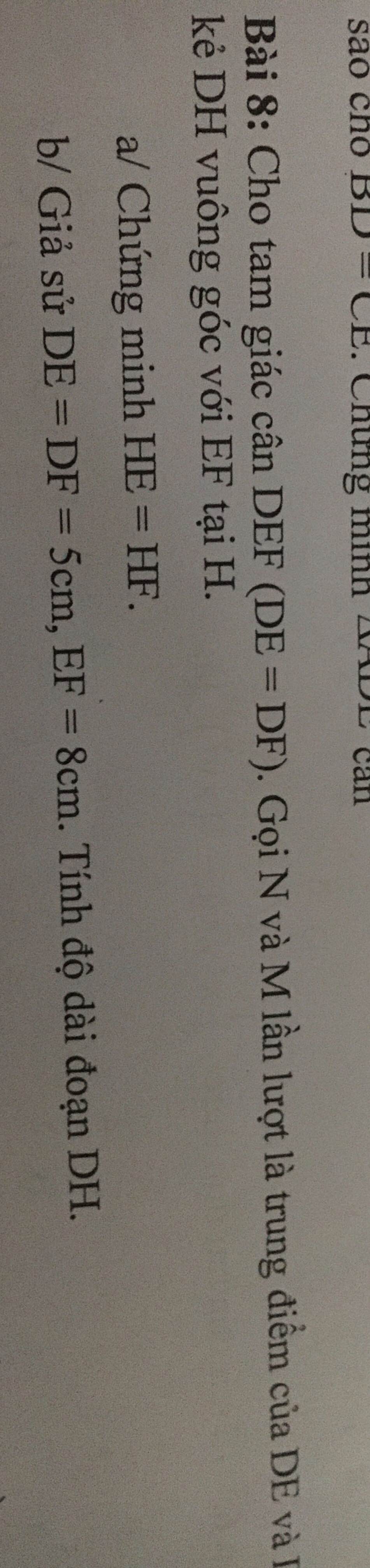
Bài này thì cần gì cho M,N...
Bạn tự xử cái hình nha :>
Ta có: \(\Delta DEF\)cân tại \(D\Rightarrow DH\)vừa là đường cao vừa là trung tuyến
\(\Rightarrow EH=HF=\frac{EF}{2}=\frac{8}{2}=4\left(cm\right)\)
Tới đây bạn xét pytago cho \(\Delta DEH\)là được nhé!