160 chia cho 5% bằng bao nhiêu làm cách nào bằng 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



10% cua 360 la 36
10% cua 360 la 36
10% cua 360 la 36
2% cua 360 la 7,2
5% cua 360 la 18
Vay 32,5% cua 360 la 133,2
dung 100%
10% của 360 là 36
20% của 360 là 72
2,5% của 360 là 9
Vậy 32,5% của 360 là 117

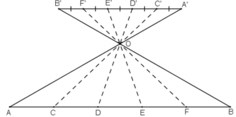
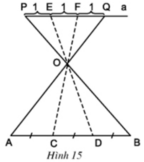
a) - Mô tả cách làm:
+ Vẽ đoạn thẳng PQ song song với AB, PQ có độ dài bằng 3 đơn vị.
+ E, F nằm trên PQ sao cho PE = EF = FQ = 1. Xác định giao điểm O của hai đoạn thẳng PB và QA
+ Vẽ các đường thẳng EO, FO cắt AB tại C và D.
Khi đó ta được AC = CD = DB.
- Chứng minh AC = CD = DB:
Theo hệ quả định lý Ta-let ta có:
ΔOAC có FQ // AC (F ∈ OC, Q ∈ OA) ⇒ 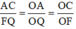
ΔOCD có EF // CD (E ∈ OD, F ∈ OC) ⇒ 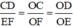
ΔODB có PE // BD (P ∈ OB, E ∈ OD) ⇒ 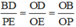
Từ 3 đẳng thức trên suy ra 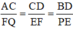
Mà FQ = EF = PE ⇒ AC = CD = DB (đpcm).
b) Tương tự chia đoạn thẳng AB thành 5 đoạn bằng nhau thực hiện như hình vẽ sau
Ngoài cách trên, ta có thể chia một đoạn thẳng thành 5 đoạn bằng nhau bằng cách vẽ thêm một đoạn thẳng AC bằng 5 đơn vị, chia đoạn thẳng AC thành 5 đoạn thẳng bằng nhau, mỗi đoạn bằng 1 đơn vị: AD = DE = EF = FG = GC.
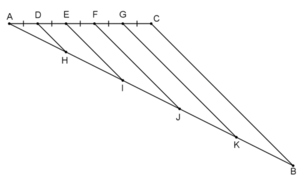
Từ các điểm D, E, F, G ta kẻ các đường thẳng song song với BC, cắt AB tại H, I, J, K. Khi đó ta thu được các đoạn thẳng AH = HI = IJ = JK = KB.

Bài 2:
a)105-(x+7)=27:25
=>105-(x+7)=22
=>x+7=105-4
=>x+7=101
=>x=94
b. (2x -8) . 2 = 24
=>4x-16=16
=>4x=32
=>x=8
bài 2:
a) \(105-\left(x+7\right)=2^7:2^5\)
\(105-\left(x+7\right)=2^2\)
\(x+7=105-4\)
\(x+7=101\)
\(x=101-7\)
\(x=94\)
b) \(\left(2x-8\right).2=2^4\)
\(\left(2x-8\right).2=16\)
\(2x-8=16:2\)
\(2x-8=8\)
\(2x=8+8\)
\(2x=16\)
\(x=8\)
bài 1:
a) \(24:\left\{390:\left[500-\left(160+30.7\right)\right]\right\}\)
\(=24:\left\{390:\left[500-\left(160+210\right)\right]\right\}\)
\(=24:\left\{390:\left[500-370\right]\right\}\)
\(=24:\left\{390:130\right\}\)
\(=24:3=8\)
b) \(120-\left[98-\left(16-9\right)^2\right]\)
\(=120-\left[98-\left(256-81\right)\right]\)
\(=120-\left[98-175\right]\)
\(=120-\left(-77\right)\)
\(=120+77=197\)
bài 3 từ từ suy nghĩ hãng like nha

Bài 1 : Gọi số tự nhiên cần tìm là : a ( a \(\in\) N* )
Theo đề ra , ta có :
\(a⋮8,a⋮10,a⋮15\Rightarrow a\in BC\left(8,10,15\right)\)
\(8=2^3\)
\(10=2.5\)
\(15=3.5\)
\(BCNN\left(8,10,15\right)=2^3.3.5=120\)
Mà : \(B\left(120\right)=\left\{0;120;...;1080;1200;1320;1440;1560;1680;1800;1920;...\right\}\)
\(\Rightarrow a\in\left\{1080;1200;1320;1440;1560;1680;1800;1920\right\}\)
Vậy ...
Bài 2 : Gọi độ dài của cạnh hình vuông là : a ( a \(\in\) N* )
Theo đề ra , ta có :
\(52⋮a,36⋮a\)
Mà : a lớn nhất
\(\Rightarrow a=ƯCLN\left(52,36\right)\)
\(52=2^2.13\)
\(36=2^2.3^2\)
\(ƯCLN\left(52,36\right)=2^2=4\)
Vậy chia 4 thì độ dài cạnh hình vuông là lớn nhất và bằng 4
ta lấy : 160 : 100 x 5
150/100*5=8