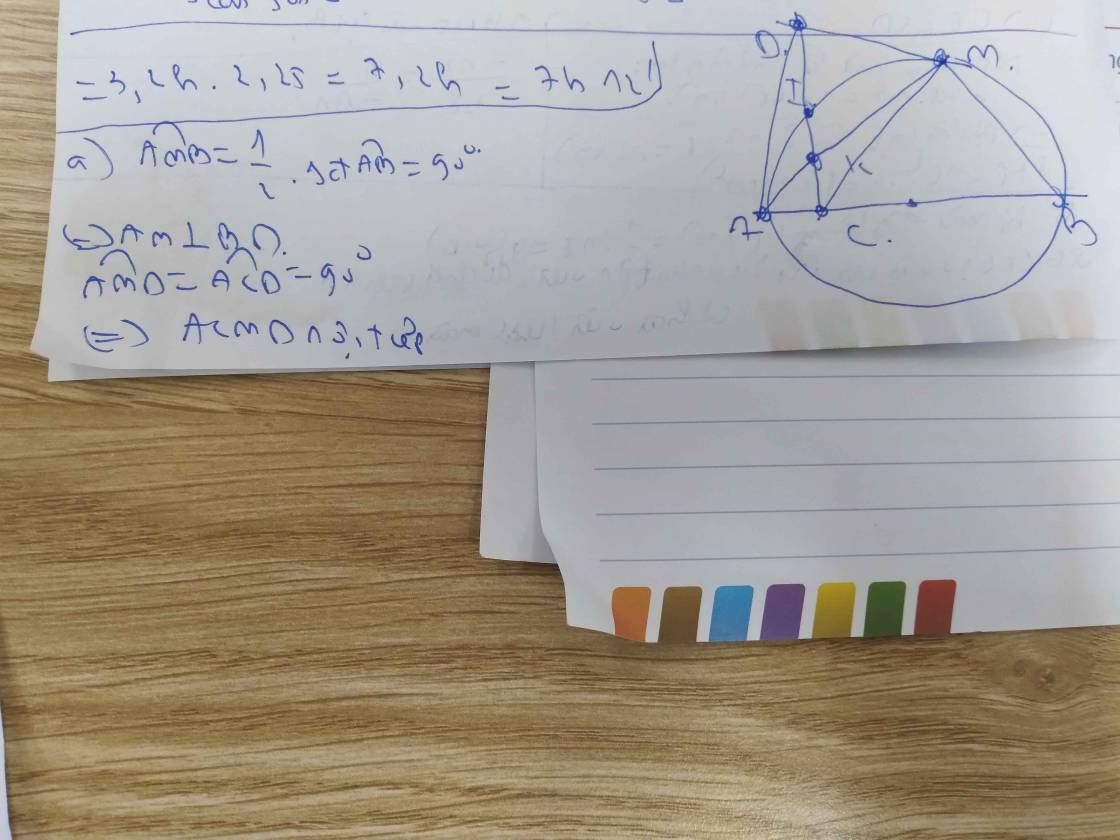
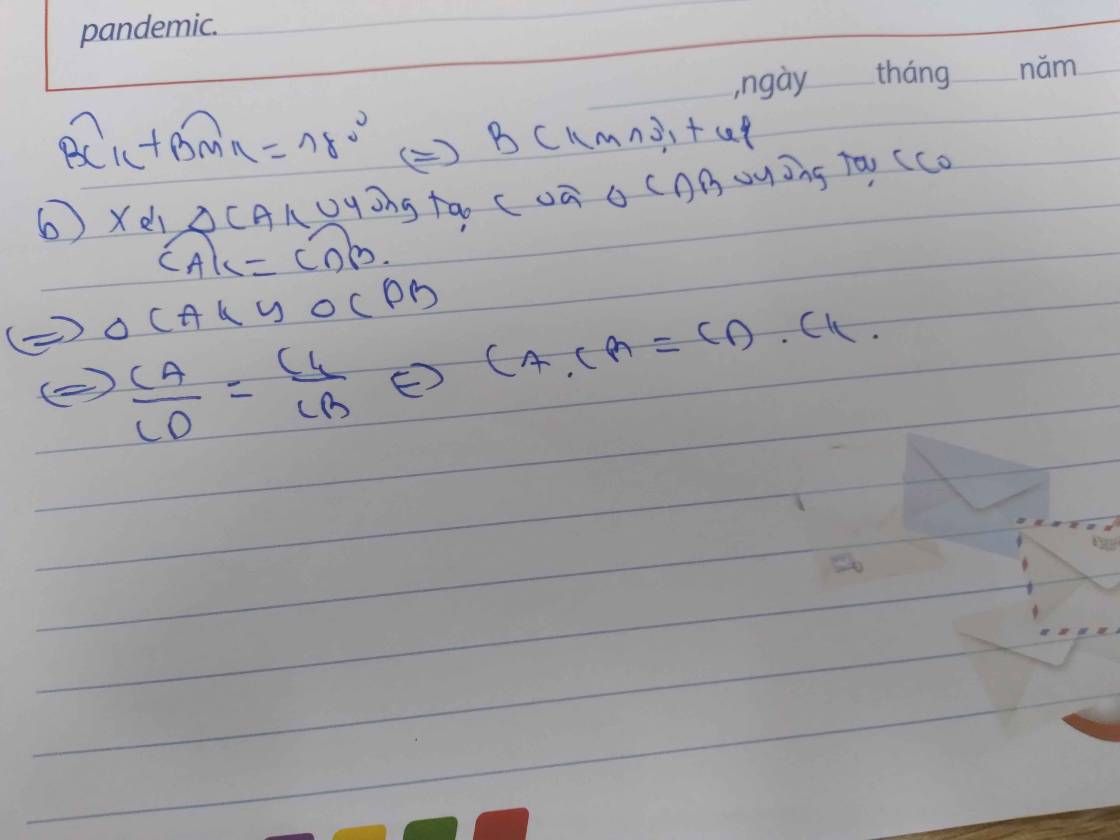Cho nửa đường tròn (O) đường kính AB, C là một điểm nằm trên đường tròn ( C khác A,B) (BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 3 2023
1:
góc AMB=1/2*sđ cung AB=90 độ
=>AM vuông góc BD
góc ACD=góc AMD=90 độ
=>ACMD nội tiếp
góc KCB+góc KMB=180 độ
=>BMKC nội tiếp
2: Xét ΔCAK vuông tại C và ΔCDB vuông tại C có
góc CAK=góc CDB
=>ΔCAK đồng dạng với ΔCDB
=>CA/CD=CK/CB
=>CA*CB=CD*CK
8 tháng 12 2023
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
=>BC\(\perp\)AC tại C
=>BC\(\perp\)AE tại C
=>ΔCEF vuông tại C
Xét (O) có
\(\widehat{ICB}\) là góc tạo bởi tiếp tuyến CI và dây cung CB
\(\widehat{CAB}\) là góc nội tiếp chắn cung CB
Do đó: \(\widehat{ICB}=\widehat{CAB}\)
mà \(\widehat{CAB}=\widehat{BFD}\left(=90^0-\widehat{CBA}\right)\)
nên \(\widehat{ICB}=\widehat{BFD}\)
mà \(\widehat{BFD}=\widehat{IFC}\)(hai góc đối đỉnh)
nên \(\widehat{ICB}=\widehat{IFC}\)
=>\(\widehat{ICF}=\widehat{IFC}\)
=>IC=IF
Ta có: \(\widehat{ICF}+\widehat{ICE}=\widehat{ECF}=90^0\)
\(\widehat{IFC}+\widehat{IEC}=90^0\)(ΔECF vuông tại C)
mà \(\widehat{ICF}=\widehat{IFC}\)
nên \(\widehat{ICE}=\widehat{IEC}\)
=>IC=IE
mà IC=IF
nên IE=IF
=>I là trung điểm của EF
b: Vì ΔCEF vuông tại C
nên ΔCEF nội tiếp đường tròn đường kính EF
=>ΔCEF nội tiếp (I)
Xét (I) có
IC là bán kính
OC\(\perp\)CI tại C
Do đó: OC là tiếp tuyến của (I)
4 tháng 10 2021
a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: DM=DB
Ta có: CM+MD=CD
mà CM=CA
và DM=DB
nên CD=CA+DB