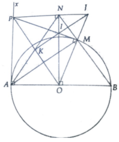
Cho đường tròn (O) đường kính AB.Kẻ tia Ax là tiếp tuyến của đường tròn (O).Trên tia Ax lấy điểm P(AP>OA).Từ P kẻ tiếp tuyến PE(E là tiếp điểm) của (O).Cho PE cắt AB tại F
a)chứng minh A,P,E,O cùng thuộc 1 đường tròn
b)chứng minh PO song song BE
c)đường thẳng vuông góc với OP tại O cắt PF tại M.Cm EM.PF=PE.MF

a: Xét tứ giác PAOE có góc PAO+góc PEO=180 độ
nên PAOE là tứ giác nội tiếp
b: Xét (O) có
PA,PE là tiếp tuyến
nên PA=PE
mà OA=OE
nên OP là trung trực của AE
=>OP vuông góc với AE
Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đo: ΔAEB vuông tại E
=>BE//OP