rút gọn rồi tính giá trị của biểu thức x(x-y)+y(x+y)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x(x – y) + y(x + y)
= x.x – x.y + y.x + y.y
= x2 – xy + xy + y2
= x2 + y2.
Tại x = –6 ; y = 8, giá trị biểu thức bằng : (–6)2 + 82 = 36 + 64 = 100.

\(\dfrac{x+y}{2\left(x+y\right)}=\dfrac{0}{2.0}=\dfrac{0}{0}???\)
\(A=\dfrac{x+y}{2\left(x+y\right)}\left(đk:x+y\ne0\right)\)
Vậy với \(x+y=0\) thì \(A\in\varnothing\)

x.(x2 – y) – x2.(x + y) + y.(x2 – x)
= x.x2 – x.y – (x2.x + x2.y) + y.x2 – y.x
= x3 – xy – x3 – x2y + x2y – xy
= (x3 – x3) + (x2y – x2y) – xy – xy
= –2xy
Tại 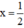 và y = –100, giá trị biểu thức bằng:
và y = –100, giá trị biểu thức bằng: 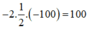

a) x(x – y) + y (x + y) = x2 – xy +yx + y2= x2+ y2
với x = -6, y = 8 biểu thức có giá trị là (-6)2 + 82 = 36 + 64 = 100

Ta có :
\(x\times\left(x-y\right)+y\times\left(x+y\right)=x^2-xy+xy+y^2=x^2+y^2\)
Thay x= -6 , y= 8 .Ta có:
\(x^2+y^2=\left(-6\right)^2+8^2=36+64=100\)
Vậy \(x\times\left(x-y\right)+y\times\left(x+y\right)=100\)
\(x\left(x-y\right)+y\left(x+y\right)\)
=\(x.x-y+y.x+y\)
=\(\left(x.x.x\right)+\left(-y+y+y\right)\)
=\(x^3+y\)
Thay x=-6 và y=8 vào biểu thức \(x^3+y\) ta được
\(x^3+y=\left(-6^3\right)+8=-208\)
Vậy -208 là giá trị của biểu thức \(x^3+y\) tại x=-6 và y=8

x( x^2 - y ) - x^2 ( x + y ) + y( x^2 - x )
=x3-xy-x3-x2y+x2y-xy
=-2xy

\(x^2+2xy+y^2-2x-2y=\left(x+y\right)^2-2\left(x+y\right)=\left(-6\right)^2-2.\left(-6\right)=\)
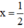 và y = –100;
và y = –100;
x(x-y) + y( x +y)
= x^2 - xy + xy + y^2
= x^2 + y^2