\(\dfrac{x}{0}\) và x - 1 đâu không phải là phân thức đại số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: P(\( - \dfrac{1}{8}\)) = 4.(\( - \dfrac{1}{8}\))+ \(\dfrac{1}{2}\)= (-\(\dfrac{1}{2}\)) + \(\dfrac{1}{2}\) = 0
Vậy \(x = - \dfrac{1}{8}\) là nghiệm của đa thức P(x) = 4x + \(\dfrac{1}{2}\)
b) Q(1) = 12 +1 – 2 = 0
Q(-1) = (-1)2 + (-1) – 2 = -2
Q(2) = 22 + 2 – 2 = 4
Vì Q(1) = 0 nên x = 1 là nghiệm của Q(x)

- Phân thức đại số (phân thức) là một biểu thức có dạng
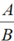
trong đó A, B là những đa thức, B ≠ 0. A là tử thức, B là mẫu thức.
- Một đa thức được coi như một phân thức với mẫu thức bằng 1.
- Một số thực a bất kì cũng là một phân thức đại số.

-Định nghĩa:Một phân thức đại số(hay nói gọn là phân thức)là một biểu thức có dạng\(\dfrac{A}{B}\),trong đó A,B là những đa thức và B khác đa thức 0.A được gọi là tử thức (hay tử) , B gọi là mẫu thức (hay mẫu).
-Mỗi đa thức cũng được coi như một phân thức với mẫu thức bằng 1.
-Chỉ có số 0, số 1 là những phân thức đại số.
*Một phân thức đại số(hay nói gọn là phân thức)là một biểu thức có dạng A/B,trong đó A,B là những đa thức và B khác đa thức 0.A được gọi là tử thức (hay tử) , B gọi là mẫu thức (hay mẫu).
-Mỗi đa thức cũng được coi như một phân thức với mẫu thức bằng 1.
-Chỉ có số 0, số 1 là những phân thức đại số.

1.Đại lượng y là hàm số của đại lượng x vì ta có mỗi giá trị của đại lượng x đều có một giá trị tương ứng của đại lượng y . Giá trị tương ứng ấy của đại lượng y là duy nhất.
2. Đại lượng y không phải là hàm số của đại lượng x vì ứng với giá trị x = 5 chẳng hạn ta có hai giá trị của y (ước tự nhiên của 5 là 1 và 5)
3. Dựa vào định nghĩa các phép toán về số hữu tỉ. Chú ý rằng với các số hữu tỉ thì kết quả của các phép toán này là số hữu tỉ. Chẳng hạn câu b). Giả sử tích của số hữu tỉ \(x\ne0\)với số vô tỉ y là số hữu tỉ z. Ta có x.y=z.
Như vậy thì \(y=\frac{z}{x}\). Nhưng z và x \(\left(x\ne0\right)\)là hai số hữu tỉ nên thương của chúng cũng là số hữu tỉ. Suy ra y là số hữu tỉ, trái với đề bài. Vậy tích của một số hữu tỉ khác 0 với một số vô tỉ là một số vô tỉ.
\(\dfrac{x}{0}\)