Tìm 1 số có 2 chữ số có chữ số hàng đơn vị gấp 4 lần chữ số hàng chục. Nếu đổi chỗ hai chữ số cho nhau thì số đó tăng lên 54 đơn vị.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 12 2016
a x 10 + b + 54 = b x 10 + a
a x 10 + a x 4 + 54 = a x 40 + a
a x 14 + 54 = a x 41
a x 27 = 54
a = 2
b = 8
Suy ra \(\overline{ab}=28\)
31 tháng 12 2016
số đó là 54 vì:
28 đảo ngược lại sẽ được 82 và hơn số cũ 54 đơn vị
9 tháng 8 2016
Gọi chữ số hàng đơn vị là x ( 0 < x <9 ) => chữ số hàng chục là 3x
Số ban đầu có dạng : 10.3x + x = 31x
Sau khi đổi chỗ số mới có dạng : 10.x + 3x = 13x
Vì số mới nhỏ hơn số đã cho 18 nên có pt 31x - 13x = 18 <=> 18x = 18 => x = 1
Suy ra chữ số hàng chục là 3. Vậy số cần tìm là 31.
23 tháng 4 2021
Ta có các số tự nhiên có 2 chữ số mà chữ só hàng đơn vị gấp ba lần chữ số hàng chục là 39;26;13
ta lần lượt thử các số
viết ngược của 13 là 31, lớn hơn số ban đầu : 31-13=18 (loại)
viết ngược của 26 là 62, lớn hơn số ban đầu :62-26=36 (loại)
viết ngược của 39 là 93, lớn hơn số ban đầu :93-39=54 (thỏa mãn)
Vậy số cần tìm là 39
CM
19 tháng 8 2019
Gọi số cần tìm là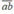 
= 10a + b (a, b ∈ N. 0 < a < b < 10)
Ta có b = 3a
Khi đổi hai chữ số ta được số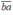 
= 10b + a
Vì số mới lớn hơn số cũ 54 đơn vị nên ta có phương trình: 10b + a – 54 = 10a + b
⇔ 9b – 9a = 54
⇔ 9.3a – 9a = 54
⇔ 18a = 54
⇔ a =3 (tmđk)
Vậy số ban đầu cần tìm là 39.