cho hình chóp sabcd có đấy là hình vuông tâm o canh=x ,gọi h là trung điểm của oa,biết sh vuông góc với abcd,sh=x.Tính góc giữa ac với sbc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp AD\\AB\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
Mà \(AD\in\left(SAD\right)\Rightarrow\left(SAD\right)\perp\left(SAB\right)\)
b.
M là điểm nào nhỉ?
c.
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\\HK\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SHK\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SKH}\) là góc giữa (SCD) và (ABCD)
\(HK=AD=a\Rightarrow tan\widehat{SKH}=\dfrac{SH}{HK}=\dfrac{\sqrt{3}}{3}\Rightarrow\widehat{SKH}=30^0\)
d.
Từ H kẻ \(HE\perp SK\) (E thuộc SK)
\(CD\perp\left(SHK\right)\) theo cmt \(\Rightarrow CD\perp HE\)
\(\Rightarrow HE\perp\left(SCD\right)\Rightarrow HE=d\left(H;\left(SCD\right)\right)\)
Hệ thức lượng:
\(\dfrac{1}{HE^2}=\dfrac{1}{SH^2}+\dfrac{1}{HK^2}\Rightarrow HE=\dfrac{a}{2}\)

Khá là dài, mình tìm ra được bằng \(\dfrac{3\sqrt3}{64}a^3\)

xin lỗi mình chép thiếu đề H là trung điểm AB và SH bằng a và vuông góc với đáy
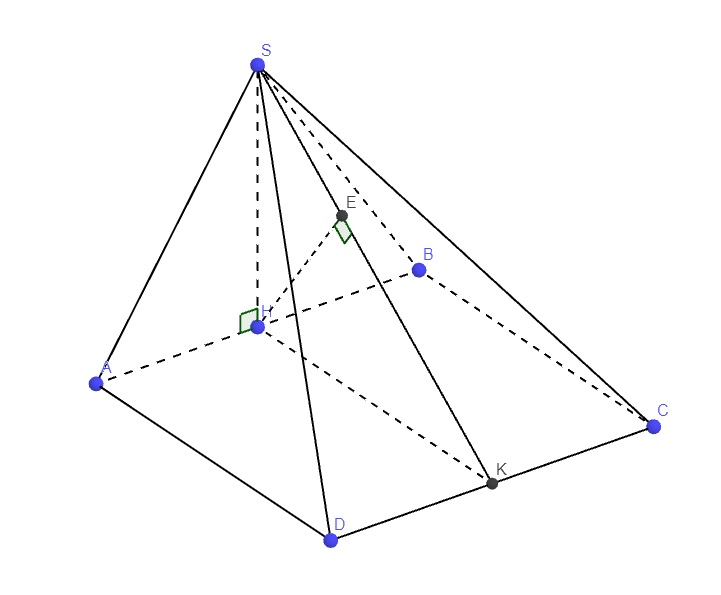

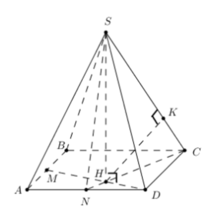

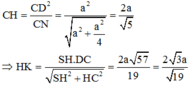
@Nguyễn Việt Lâm giúp e với
Qua H kẻ đường thẳng song song AB cắt BC tại M
\(\Rightarrow BC\perp\left(SHM\right)\)
Trong mp (SHM), từ H kẻ \(HK\perp SM\Rightarrow HK\perp\left(SBC\right)\)
\(\Rightarrow\widehat{HCK}\) là góc giữa AC và (SBC) (do H nằm trên AC)
\(\dfrac{MH}{AB}=\dfrac{CH}{AC}=\dfrac{3}{4}\Rightarrow MH=\dfrac{3x}{4}\)
\(\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{HM^2}\Rightarrow HK=\dfrac{SH.MH}{\sqrt{SH^2+MH^2}}=\dfrac{3x}{5}\)
\(HC=\dfrac{3}{4}AC=\dfrac{3x\sqrt{2}}{4}\)
\(sin\widehat{HCK}=\dfrac{HK}{HC}=\dfrac{2\sqrt{2}}{5}\Rightarrow\widehat{HCK}\approx34^027'\)