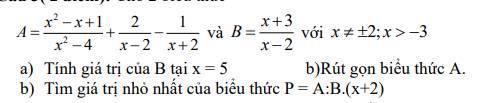
Giải hộ mình chi tiết câu tìm giá trị nhỏ nhất nha.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=x^2-6x+11\)
\(\Leftrightarrow A=x^2-2.3x+9+2\)
\(\Leftrightarrow A=\left(x-3\right)^2+2\ge2\)
\(\Leftrightarrow A_{min}=2\)
\(\Leftrightarrow x-3=0\)
\(x=3\)

Ta có \(\left|x+1\right|\ge0\)với mọi giá trị của x
và \(\left|x-2018\right|\ge0\)với mọi giá trị của x
=> \(\left|x+1\right|+\left|x-2018\right|\ge0\)với mọi giá trị của x
Vậy GTNN của A là 0.

Ta có: (x + 2)4 \(\ge\)0 với mọi x
|2y - 10| \(\ge\)0 với mọi y
=> (x + 2)4 + |2y - 10| \(\ge\)0
=> S = (x + 2)4 + |2y - 10| + 2017 \(\ge\)2017
Dấu "=" xảy ra <=> \(\hept{\begin{cases}\left(x+2\right)^4=0\\\left|2y-10\right|=0\end{cases}}\)<=>\(\hept{\begin{cases}x=-2\\y=5\end{cases}}\)
Vậy GTNN của S = 2017 tại x = -2 và y = 5

a/ \(M=x^2-2.\frac{3}{2}x+\left(\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2+5\)
\(=\left(x-\frac{3}{2}\right)^2+\frac{11}{4}\ge\frac{11}{4}\)
Vậy Min M = 11/4 khi x - 3/2 = 0 => x = 3/2
b/ \(N=-\left(4x^2-\frac{2}{8}x+5\right)\)
\(=-\left[\left(2x\right)^2-2.2x.\frac{1}{16}+\left(\frac{1}{16}\right)^2-\left(\frac{1}{16}\right)^2+5\right]\)
\(=-\left(2x-\frac{1}{16}\right)^2-\frac{1279}{256}\ge-\frac{1279}{256}\)
Vậy Min N = -1279/256 khi 2x - 1/16 = 0 => 2x = 1/16 => x = 1/32
Lời giải:
a.
Tại $x=5$ thì $B=\frac{5+3}{5-2}=\frac{8}{3}$
b.
\(A=\frac{x^2-x+1}{(x-2)(x+2)}+\frac{2(x+2)}{(x-2)(x+2)}-\frac{x-2}{(x-2)(x+2)}=\frac{x^2-x+1+2(x+2)-(x-2)}{(x-2)(x+2)}\)
\(=\frac{x^2+7}{(x-2)(x+2)}\)
c.
\(P=A:B(x+2)=\frac{x^2+7}{(x-2)(x+2)}:\frac{x+3}{x-2}.(x+2)=\frac{x^2+7}{x+3}\)
Áp dụng BĐT Cô-si:
$x^2+1\geq 2|x|\geq 2x$
$\Rightarrow x^2+7\geq 2x+6=2(x+3)$
$\Rightarrow P\geq \frac{2(x+3)}{x+3}=2$
Vậy $P_{\min}=2$. Giá trị này đạt tại $x^2=1\Leftrightarrow x=\pm 1$ (tm)