Cho ∆ABC lấy M,N,P lần lượt trên các cạnh BC,CA,AB sao cho AM ,BN,CP cắt nhau tại O qua A và C . Vẽ các đoạn thẳng song song với BO cắt CO, OA ở E và F.
a) C/m ∆ FCM ~∆OMB và ∆PAE ~∆PBO.
b)C/m MB/MC * NC/NA*PA/PB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 3 2020
Câu a dễ..Câu b
Qua A kẻ đ/thẳng //BC cắt CO,BO tại H,K
Có HK//BC nên ta có các hệ thức sau
\(\frac{MB}{MC}=\frac{AK}{AH}\left(1\right)\),\(\frac{NC}{NA}=\frac{BC}{AK}\left(2\right)\),\(\frac{PA}{PB}=\frac{AH}{BC}\left(3\right)\)
Nhân (1),(2) và (3) suy ra ĐPCM
18 tháng 2 2020
Xét\(\Delta\)ABC có: NE //BC; BD //BC
=> \(\frac{AN}{AB}=\frac{NE}{BC}\) và \(\frac{AM}{AB}=\frac{MD}{BC}\)
=> \(\frac{MD}{BC}+\frac{NE}{BC}=\frac{AM}{AB}+\frac{AN}{AB}\)
=> \(\frac{MD+NE}{BC}=\frac{AM+AN}{AB}=\frac{NB+AN}{AB}=\frac{AB}{AB}=1\)
=> MD + NE = BC
CM
12 tháng 6 2018
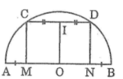
Ta có: MC // ND (gt)
Suy ra tứ giác MCDN là hình thang
Lại có: OM + AM = ON + BN (= R)
Mà AM = BN (gt)
Suy ra: OM = ON
Kẻ OI ⊥ CD (3)
Suy ra: IC = ID (đường kính dây cung)
Khi đó OI là đường trung bình của hình thang ACDN
Suy ra: OI // MC // ND (4)
Từ (3) và (4) suy ra: MC ⊥ CD, ND ⊥ CD.