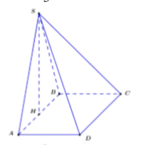
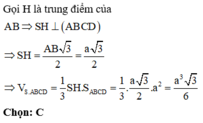
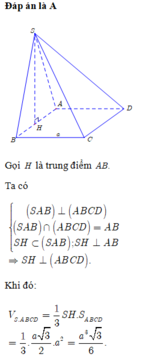
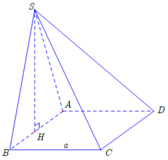
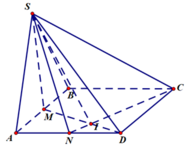
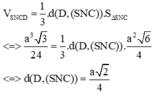1, Cho hình chóp SABCD có đáy ABCD là hình vuông . Mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với (ABCD).CÓ mấy mặt phẳng vuông góc với (sab)
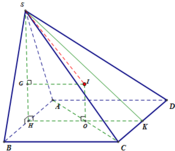
2, Cho hình chóp SABCD có đáy ABCD là hình thoi . Mặt phẳng (SAC) vuông góc (ABCD) . mệnh đề nào đúng
A. (SAC) vuông góc (SBD)
b. (SBD) vuông góc (ABCD)
C.(BCD) vuông góc (ACD)
D.(SAB) vuông góc (SAD)
3, Cho tứ diện ABCD có AB=AC=AD và tam giác BCD vuông ở B . Trong các mặt phẳng sau , cặp nào vuông góc với nhau
A.(ABC) và (ABD) B.(ABD) và (BCD)
C. (BCD) và (ACD) D.(ACD) và (ABC)
4. tứ diện abcd có bcd là tam giác vuông ở b . (ABC) vuông góc (BCD) . các cạnh của tứ diện cạnh nào là đường cao
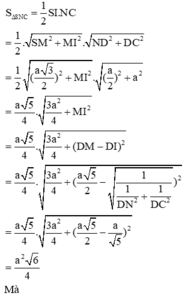
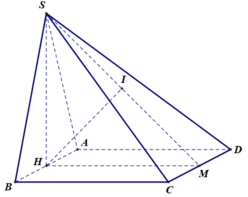
5. Cho hình chóp SABC có đáy abc là tam giác vuông ở b với AB=3a,BC=4a. biết SA vuông góc với đáy , góc giữa (SBC) và (ABC)=60 ĐỘ . TÍNH diện tích tam giác sbc