\(0,5\sqrt{100}-\dfrac{1}{4}\sqrt{16}+\left(-\dfrac{2}{3}\right)^3\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 8 2021
a)\(\dfrac{3}{4}-\dfrac{5}{2}-\dfrac{3}{5}=\dfrac{15}{20}-\dfrac{50}{20}-\dfrac{12}{20}=-\dfrac{47}{20}\)
b) \(\sqrt{7^2}+\sqrt{\dfrac{25}{16}-\dfrac{3}{2}}=7+\sqrt{\dfrac{1}{16}}=7+\dfrac{1}{4}=\dfrac{29}{4}\)
c) \(\dfrac{1}{2}.\sqrt{100}-\sqrt{\dfrac{1}{16}+\left(\dfrac{1}{3}\right)^0}=\dfrac{1}{2}.10-\sqrt{\dfrac{1}{16}+1}=5-\sqrt{\dfrac{17}{16}}\)
TT
17 tháng 12 2017
a,\(3\dfrac{17}{24}+\left(2\dfrac{8}{15}-4\dfrac{8}{15}\right):\left(2\dfrac{11}{30}-\dfrac{11}{30}\right)\)
\(=\dfrac{89}{24}-2:2\)
\(=\dfrac{65}{24}\)
b,\(0,5:\sqrt{625}-\sqrt{\dfrac{4}{25}}+0,18.\left(\sqrt{1\dfrac{9}{16}}-\sqrt{\dfrac{9}{16}}\right)\)
\(=0,5:25-\dfrac{2}{5}+0,18.\dfrac{1}{2}\)
\(=-\dfrac{29}{100}\)
8 tháng 6 2021
a,\(\left(\sqrt{1\dfrac{9}{16}}-\sqrt{\dfrac{9}{16}}\right):5=\left(\sqrt{\dfrac{25}{16}}-\dfrac{3}{4}\right):5=\left(\dfrac{5}{4}-\dfrac{3}{4}\right):5\)
\(=\dfrac{1}{2}:5=\dfrac{1}{10}\)
b,\(\left(\sqrt{3}-2\right)^2\left(\sqrt{3}+2\right)^2=\left[\left(\sqrt{3}-2\right)\left(\sqrt{3}+2\right)\right]^2\)
\(=\left[3-4\right]^2=1\)
c,\(\left(11-4\sqrt{3}\right)\left(11+4\sqrt{3}\right)=11^2-\left(4\sqrt{3}\right)^2\)
\(=121-48=73\)
d,\(\left(\sqrt{2}-1\right)^2-\dfrac{3}{2}\sqrt{\left(-2\right)^2}+\dfrac{4\sqrt{2}}{5}+\sqrt{1\dfrac{11}{25}}.\sqrt{2}\)
\(=2-2\sqrt{2}+1-3+\dfrac{4\sqrt{2}}{5}+\sqrt{\dfrac{36}{25}.2}\)
\(=-2\sqrt{2}+\dfrac{4\sqrt{2}+6\sqrt{2}}{5}\)
\(=-2\sqrt{2}+\dfrac{10\sqrt{2}}{5}=-2\sqrt{2}+2\sqrt{2}=0\)
e,\(\left(1+\sqrt{2021}\right)\sqrt{2022-2\sqrt{2021}}\)
\(=\left(1+\sqrt{2021}\right)\sqrt{2021-2\sqrt{2021}.1+1}\)
\(=\left(1+\sqrt{2021}\right)\sqrt{\left(\sqrt{2021}-1\right)^2}\)
\(=\left(1+\sqrt{2021}\right)\left(\sqrt{2021}-1\right)\)
\(=\sqrt{2021}-1+\sqrt{2021^2}-\sqrt{2021}=2020\)
25 tháng 10 2022
a: \(=2\cdot\dfrac{5}{4}-3\cdot\dfrac{7}{6}+4\cdot\dfrac{9}{8}=\dfrac{5}{2}-\dfrac{7}{2}+\dfrac{9}{2}=\dfrac{7}{2}\)
b: \(=18-16\cdot\dfrac{1}{2}+\dfrac{1}{16}\cdot\dfrac{3}{4}\)
=10+3/64
=643/64
c: \(=\dfrac{2}{3}\cdot\dfrac{9}{4}-\dfrac{3}{4}\cdot\dfrac{8}{3}+\dfrac{7}{5}\cdot\dfrac{5}{14}=\dfrac{3}{2}-2+\dfrac{1}{2}=2-2=0\)
YP
1
19 tháng 12 2021
\(=\dfrac{1}{2}\cdot10-\dfrac{1}{4}+1=6-\dfrac{1}{4}=\dfrac{23}{4}\)
DN
17 tháng 12 2021
\(\sqrt{16}.\left(\dfrac{1}{2}\right)^3+3.\left(\dfrac{1}{2}\right)^2+2.\sqrt{\dfrac{1}{4}}\)
\(\text{}4.\left(-\dfrac{1}{8}\right)+3.\left(\dfrac{1}{4}\right)+2.\left(\dfrac{1}{2}\right)\)
\(-\dfrac{1}{2}+\dfrac{3}{4}+1=\dfrac{5}{4}\)
30 tháng 6 2021
a) Ta có: \(\dfrac{-4}{3}\cdot\sqrt{\left(-0.4\right)^2}\)
\(=-\dfrac{4}{3}\cdot0.4\)
\(=\dfrac{-1.6}{3}=-\dfrac{8}{15}\)
b) Ta có: \(\sqrt[3]{\dfrac{3}{4}}\cdot\sqrt[3]{\dfrac{9}{16}}\)
\(=\sqrt[3]{\dfrac{27}{64}}=\dfrac{3}{4}\)
c) Ta có: \(\dfrac{1}{3+\sqrt{2}}+\dfrac{1}{3-\sqrt{2}}\)
\(=\dfrac{3-\sqrt{2}+3+\sqrt{2}}{7}\)
\(=\dfrac{6}{7}\)
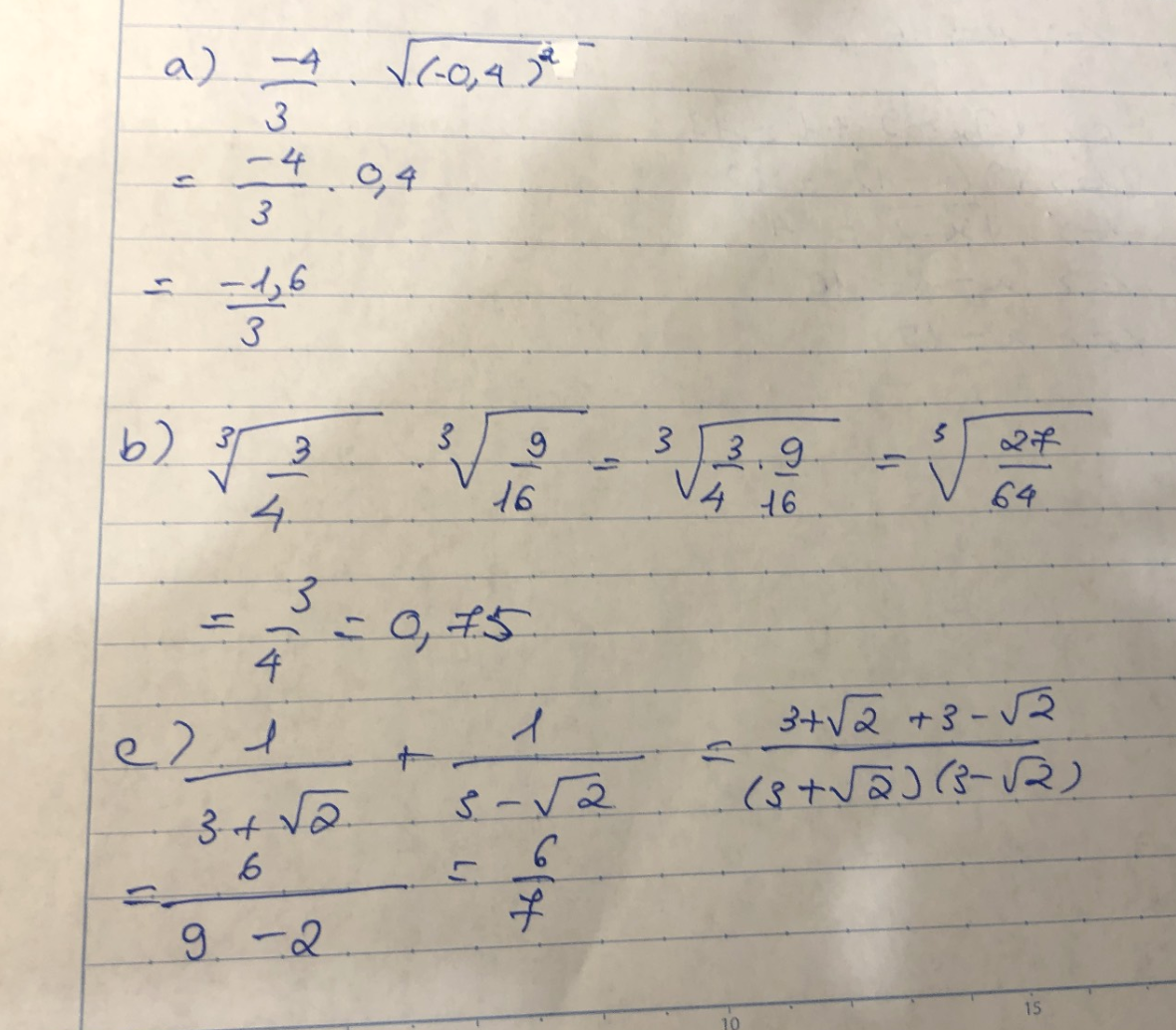
\(0,5\sqrt{100}-\dfrac{1}{4}\sqrt{16}+\left(-\dfrac{2}{3}\right)^2\\=\dfrac{1}{2}.10-\dfrac{1}{4}.4+\dfrac{4}{9}\\ =5-1+\dfrac{4}{9}\\ =4+\dfrac{4}{9}\\ =\dfrac{40}{9} \)
`(-2/3)^2` Ạ