tìm x biết 4x3+x=4x2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: P(x)=6x^3-4x^2+4x-2
Q(x)=-5x^3-10x^2+6x+11
M(x)=x^3-14x^2+10x+9
b: \(C\left(x\right)=7x^4-4x^3-6x+9+3x^4-7x^3-5x^2-9x+12\)
=10x^4-11x^3-5x^2-15x+21

Điều kiện: x 3 - 2 x 2 = x 2 x - 2 ≠ 0 ⇒ x ≠ 0 và x ≠ 2
Ta có: 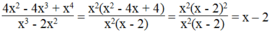
Nếu phân thức đã cho bằng 2 thì biểu thức x - 2 cũng có giá trị bằng 2. Suy ra: x- 2 = 2 ⇒ x = 4. Với x = 4 thỏa mãn điều kiện.
Vậy khi x = 4 thì phân thức có giá trị bằng 2.

Điều kiện: x 3 - 2 x 2 = x 2 x - 2 ≠ 0 ⇒ x ≠ 0 và x ≠ 2
Ta có: 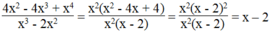
Nếu phân thức đã cho bằng -2 thì biểu thức x - 2 cũng có giá trị bằng -2. Suy ra: x - 2 = -2 ⇒ x = 0 không thỏa mãn điều kiện.
Vậy không có giá trị nào của x để phân thức bằng -2

\(\Leftrightarrow4x^2\left(x-1\right)-\left(x-1\right)=0\Leftrightarrow\left(2x-1\right)\left(2x+1\right)\left(x-1\right)=0\Leftrightarrow x=\dfrac{1}{2};x=-\dfrac{1}{2};x=1\)
\(4x^3-4x^2-x+1=0\)
<=>\(\left(2x+1\right)\left(x-1\right)\left(2x-1\right)=0\)
<=>\(\left[{}\begin{matrix}x=\dfrac{-1}{2}\\x=1\\x=\dfrac{1}{2}\end{matrix}\right.\)

Điều kiện: x 3 - 2 x 2 = x 2 x - 2 ≠ 0 ⇒ x ≠ 0 và x ≠ 2
Ta có: 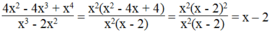
Nếu phân thức có giá trị bằng 0 thì biểu thức x - 2 cũng có giá trị bằng 0. Suy ra: x - 2 = 0 ⇒ x = 2 mà x = 2 không thỏa mãn điều kiện.
Vậy không có giá trị nào của x để phân thức có giá trị bằng 0.

c: \(x^4+x^3-4x^2+x+1\)
\(=x^4-x^3+2x^3-2x^2-2x^2+2x-x+1\)
\(=\left(x-1\right)\left(x^3+2x^2-2x-1\right)\)
\(=\left(x-1\right)\left[\left(x-1\right)\left(x^2+x+1\right)+2x\left(x-1\right)\right]\)
\(=\left(x-1\right)^2\cdot\left(x^2+3x+1\right)\)

\(a,P\left(x\right)=2x^3-x+x^2-x^3+3x+5\\ =\left(2x^3-x^3\right)+x^2+\left(-x+3x\right)+5\\ =x^3+x^2+2x+5\\ Q\left(x\right)=3x^3+4x^2+3x-4x^3-5x^2+10\\ =\left(3x^3-4x^3\right)+\left(4x^2-5x^2\right)+3x+10\\ =-x^3-x^2+3x+10\\ b,M\left(x\right)=P\left(x\right)+Q\left(x\right)=x^3+x^2+2x+5-x^3-x^2+3x+10\\ =\left(x^3-x^3\right)+\left(x^2-x^2\right)+\left(2x+3x\right)+\left(5+10\right)=5x+15\\ N\left(x\right)=P\left(x\right)-Q\left(x\right)=x^3+x^2+2x+5-\left(-x^3-x^2+3x+10\right)\\ =x^3+x^2+2x+5+x^3+x^2-3x-10\\ =\left(x^3+x^3\right)+\left(x^2+x^2\right)+\left(2x-3x\right)+\left(5-10\right)\\ =2x^3+2x^2-x-5\)
`a,P(x)= 2x^3 -x+x^2 -x^3 +3x+5`
`= (2x^3 -x^3)+x^2+(-x+3x) +5`
`= x^3 +x^2 + 2x+5`
`Q(x)=3x^3 +4x^2+3x-4x^3-5x^2+10`
`= (3x^3-4x^3)+(4x^2-5x^2)+3x+10`
`= -x^3 -x^2+3x+10`
`b,M(x)=P(x)+Q(x)`
`->M(x)=(x^3 +x^2 + 2x+5)+(-x^3 -x^2+3x+10)`
`=x^3 +x^2 + 2x+5+(-x^3) -x^2+3x+10`
`=(x^3 -x^3)+(x^2 -x^2)+(2x+3x)+(5+10)`
`= 5x+15`
`N(x)=P(x)-Q(x)`
`->N(x)=(x^3 +x^2 + 2x+5)-(-x^3 -x^2+3x+10)`
`=x^3 +x^2 + 2x+5-x^3 +x^2-3x-10`
`=(x^3-x^3)+(x^2+x^2)+(2x-3x)+(5-10)`
`=2x^2 -x-5`

* f(x) = x2 + 2x3− 7x5 − 9 − 6x7 + x3 + x2 + x5 − 4x2 + 3x7
= (x2+ x2 – 4x2)+ (2x3 + x3 ) - (7x5 - x5 ) – 9 – (6x7 – 3x7)
= - 2x2 + 3x3 – 6x5 – 9 – 3x7
Sắp xếp theo thứ tự tăng của biến: f(x) = −9 − 2x2 + 3x3 − 6x5 − 3x7
* g(x) = x5 + 2x3 − 5x8 − x7 + x3 + 4x2 -5x7 + x4 − 4x2 − x6 – 12
= x5+ (2x3 + x3) - 5x8 – (x7+ 5x7) + (4x2 – 4x2 ) + x4 – x6 – 12
= x5 + 3x3 – 5x8 – 6x7 + x4 – x6 – 12
Sắp xếp theo thứ tự tăng của biến: g(x) = −12 + 3x3 + x4 + x5 – x6 − 6x7− 5x8
* h(x) = x + 4x5 − 5x6 − x7 + 4x3 + x2 − 2x7 + x6 − 4x2 − 7x7 + x.
= (x+ x) +4x5 – (5x6 – x6)- (x7 + 2x7+ 7x7) + 4x3+ (x2 – 4x2)
= 2x + 4x5 - 4x6 – 10x7 + 4x3 -3x2
Sắp xếp theo thứ tự tăng của biến: h(x) = 2x − 3x2 + 4x3 + 4x5 − 4x6 − 10x7
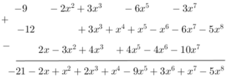
$4x^3 + x = 4x^2$
$\Leftrightarrow x(4x^2 - 4x + 1) = 0$
$\Leftrightarrow x(2x - 1)^2 = 0$
$\Leftrightarrow \left[\begin{aligned}&x = 0\\ &2x - 1 = 0\\ \end{aligned}\right. \Leftrightarrow \left[\begin{aligned}&x = 0\\ &x = \dfrac12\\ \end{aligned}\right.$