Đưa một quả đồng có khối lượng m1=1kg đã được nung nóng đến 100°C vào một thùng sắt có khối lượng m2=500g đựng 2l nước ở nhiệt độ 20°C.Bỏ qua sự trao đổi nhiệt với môi trường. a) Tính nhiệt độ cuối cùng của hệ b) Người ta lấy nước nói trên để đun đến điểm sôi.Tính nhiệt lượng cần thiết cung cấp. Giúp mình với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
13 tháng 10 2017
Đáp án : D
- Gọi t là nhiệt độ cân bằng của hệ
- Nhiệt lượng cục đồng tỏa ra khi hạ nhiệt từ 100 0 C đến t 0 C :
- Nhiệt lượng thùng sắt và nước nhận được để tăng nhiệt độ từ 20 0 C đến t 0 C :
- Theo phương trình cân bằng nhiệt , ta có:
Q 1 = Q 2 + Q 3
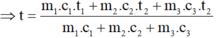
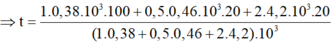
= 23 , 37 0 C
26 tháng 4 2022
Ta có phương trình cân bằng nhiệt
\(Q_{thu}=Q_{tỏa}\\ \Leftrightarrow1.4200\left(t_{cb}-30\right)=0,6.380\left(100-t_{cb}\right)\\ \Rightarrow t_{cb}=33,6^o\)
Nước nóng thêm số độ là
\(\Delta t=t_{cb}-t_1=33,6-30=3,6^o\)
19 tháng 7 2016
gọi :
Q1 là nhiệt lượng của quả cầu bằng đồng
Q2 là nhiệt lượng của quả cầu bằng nhôm
Q3 là nhiệt lượng của nhiệt lượng kế
Q4 là nhiệt lượng của nước
do không biết chất nào thu chất nào tỏa nên ta có:
\(Q_1+Q_2+Q_3+Q_4=0\)
\(\Leftrightarrow m_1C_1\left(t_1-t\right)+m_2C_2\left(t_2-t\right)+m_3C_3\left(t_3-t\right)+m_4C_4\left(t_4-t\right)=0\)
\(\Leftrightarrow380\left(100-t\right)+440\left(50-t\right)+460\left(40-t\right)+8400\left(40-t\right)=0\)
giải phương trình ta có t=42,8 độ C
21 tháng 3 2017
sao không có chất nào thu toả j nhỉ
thôi sai bạn cứ việc sửa cho mình nha
Q1+Q2+Q3+Q4=0
=>380(100-t)+880.0,5(50-t)+460(40-t)+2.4200(40-t)=0
=38000-380t+22000-440t+18400-460t+336000-8400t=0
=414400=9680t
=t=42.8độ
H9
HT.Phong (9A5)
CTVHS
30 tháng 3 2023
Nhiệt độ cuối cùng của hệ khi cân bằng nhiệt là:
\(Q_1+Q_2+Q_3+Q_4=0\)
\(=m_1c_1\left(t-t_1\right)+m_2c_2\left(t-t_2\right)+m_3c_3\left(t-t_3\right)+m_4c_4\left(t-t_4\right)=0\)
\(=1.380.\left(t-100\right)+0,5.880.\left(t-50\right)+0,4.460.\left(t-40\right)+2.4200.\left(t-40\right)=0\)
\(=380\left(t-100\right)+440\left(t-50\right)+184\left(t-40\right)+8400\left(t-40\right)=0\)
\(=380t-38000+440t-22000+184t-7360+8400t-336000=0\)
\(=9404t-403360=0\)
\(\Leftrightarrow9404t=403360\)
\(\Leftrightarrow t=\dfrac{403360}{9404}\approx43^oC\)
25 tháng 4 2023
Tóm tắt
\(m_1=500g=0,5kg\)
\(t_1=100^0C\)
\(m_2=2kg\)
\(t_2=25^0C\)
\(c_1=380J/kg.K\)
\(c_2=4200J/kg.K\)
________________
\(t=?^0C\)
Giải
Theo phương trình cân bằng nhiệt ta có:
\(Q_1=Q_2\)
\(\Leftrightarrow m_1.c_1.\left(t_1-t\right)=m_2.c_2.\left(t-t_2\right)\)
\(\Leftrightarrow0,5.380.\left(100-t\right)=2.4200.\left(t-25\right)\)
\(\Leftrightarrow t=26,6^0C\)
8 tháng 5 2022
Gọi nhiệt độ nước ban đầu là \(t_2^oC\).
Nhiệt lượng miếng đồng tỏa ra:
\(Q_{toả}=m_1c_1\left(t_1-t\right)=0,6\cdot380\cdot\left(100-30\right)=15960J\)
Nhiệt lượng nước thu vào:
\(Q_{thu}=m_2c_2\left(t-t_2\right)=2,5\cdot4200\cdot\left(30-t_2\right)J\)
Cân bằng nhiệt: \(Q_{tỏa}=Q_{thu}\)
\(\Rightarrow15960=2,5\cdot4200\cdot\left(30-t_2\right)\Rightarrow t_2=28,48^oC\)
Nước nóng thêm \(\Delta t_2=30-28,48=1,52^oC\)
29 tháng 4 2023
Tóm tắt
\(m_1=500g=0,5kg\\ t_1=100^0C\\ m_2=3kg\\ t=35^0C\\ \Rightarrow\Delta t_1=t_1-t=100-35=65^0C\\ c_1=380J/kg.K\\ c_2=4200J/kg.K\)
________________
\(\Delta t_2=?^0C\)
Giải
Nhiệt độ nước nóng thêm là:
Theo phương trình cân bằng nhiệt ta có:
\(Q_1=Q_2\\ \Leftrightarrow m_1.c_1.\Delta t_1=m_2.c_2.\Delta t_2\\\Leftrightarrow0,5.380.65=3.4200. \Delta t_2\\ \Leftrightarrow12350=12600\Delta t_2\\ \Delta t_2=1^0C\)
A
29 tháng 4 2023
Tóm tắt: Giải
m1= 500g=0,5kg Nhiệt lượng miếng đồng toả ra là:
m2= 3kg Q1= 0,5.(100-35).380 = 12 350 (J)
t1=100°C Áp dụng phương trình cân bằng nhiệt ta có:
t=35°C Q1 = Q2 = 3. △2.4200 = 12 350 (J)
c1= 380J/kg.K => △t = \(\dfrac{12350}{3.4200}\) =1,47 (°C)
c2= 4200J/kg.K Vậy miếng đồng tăng lên 1,47°C
____________
△t = ? (°C)