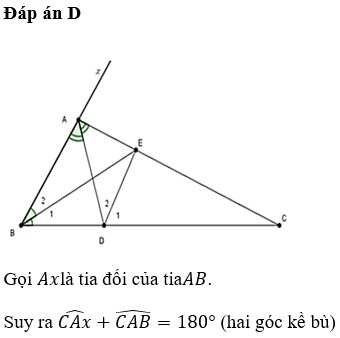
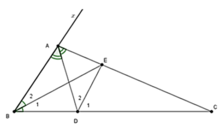
Cho tam giác ABC có góc A = 120 độ , các đường phân giác AD và BE . Tính số đo góc BED
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 3 2020
Bạn tự vẽ hình nhé!
a)Xét tam giác BAD có góc BAD=60o=1/2.BAC=1/2.120o
suy ra đc AC là phân giác góc ngoài của tam giác BAD( góc ngoài của BAD tại đỉnh A=120o)
mà AE,BE.DE đồng quy tại một điểm
BE là phân giác trong của tam giác ABD
suy ra DE là phân giác góc ngoài
b) CM tương tự câu a, ta sẽ có DF cũng là phân giác góc ngoài của tam giác ACE
FDA+ADE=1/2.BDA+1/2.CDA=1/2(BDA+CDA)=1/2.180o=90o
còn câu cuối mk chưa nghĩ ra, khi nào có gửi bạn sau nha!
AI
2
4 tháng 3 2018
kẻ̉̉̉ tia Ax là tia đố́́́́́i củ̉̉̉a tia AC góc CAB=120 độ̣ =2góc CAD=2DAB => góc xAC =60 độ =>AC là pg củ̉̉a xAD; BE là pg cua gócABC mà BE cắt AC tạ̣i E =>DElà pg cua góc ADC =>góc DEB =góc EDC - EDB = ADC/2 - ABD/2 =120 - ADC/2 -60 - ACD/2 =120 /2 -60/2=30độ̣
25 tháng 4 2019
kẻ̉̉̉ tia Ax là tia đố́́́́́i củ̉̉̉a tia AC \(\widehat{CAB}=120^o\)\(=2\widehat{CAD}=2\widehat{DAB}\) \(\Rightarrow\widehat{XAC}=60^o\) =>AC là phân giác củ̉̉a \(\widehat{XAD}\); BE là phân giác của \(\widehat{ABC}\) mà BE cắt AC tạ̣i E =>DE là phân giác cua \(\widehat{ADC}\) \(\Rightarrow\widehat{DEB}=\widehat{EDC}-\widehat{EDB}\) = \(\widehat{\frac{ADC}{2}}-\widehat{\frac{ABD}{2}}\) \(=120^o-\widehat{\frac{ADC}{2}}-60^o-\frac{\widehat{ACD}}{2}\) \(=\frac{120^o}{2}-\frac{60^o}{2}=30^o\)
