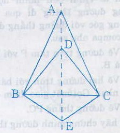
Cho tam giác cân ABC,DBC,EBC chung đáy BC.Chứng minh rằng ba điểm A,D,E thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 4 2016
Vì ∆ABC cân tại A => AB = AC
=> A thuộc trung trực của BC
Vì ∆DBC cân tại D => DB = DC
=> D thuộc trung trực của BC
Vì ∆EBC cân tại E => EB = EC
=> E thuộc trung trực của BC
Do đó A, D, E thuộc đường trung trực của BC nên A, D, E thẳng hàng.
3 tháng 5 2016
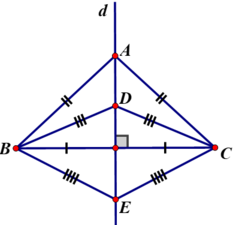
Gọi d là đường trung trực của đoạn thẳng BC theo định lí 2 :
AB=AC => A thuộc d
DB=DC => D thuộc d
EC=EB => E thuộc d
Các điểm A D E cùng thuộc đường thẳng d. Vậy A D E thẳng hàng
CM
12 tháng 5 2017
Tam giác ABC cân tại A nên AB = AC
Khi đó A thuộc đường trung trực của BC (1)
Tam giác DBC cân tại D nên DB = DC
Khi đó D thuộc đường trung trực của BC (2)
Tam giác EBC cân tại E nên EB = EC
Khi đó E thuộc đường trung trực của BC (3)
Từ (1), (2) và (3) suy ra: A, D, E thẳng hàng.
12 tháng 4 2018
Vì ∆ABC cân tại A => AB = AC
=> A thuộc trung trực của BC
Vì ∆DBC cân tại D => DB = DC
=> D thuộc trung trực của BC
Vì ∆EBC cân tại E => EB = EC
=> E thuộc trung trực của BC
Do đó A, D, E thuộc đường trung trực của BC nên A, D, E thẳng hàng
CM
20 tháng 9 2017
Vì ΔABC cân tại A ⇒ AB = AC
⇒ A thuộc đường trung trực của BC.
Vì ΔDBC cân tại D ⇒ DB = DC
⇒ D thuộc đường trung trực của BC
Vì ΔEBC cân tại E ⇒ EB = EC
⇒ E thuộc đường trung trực của BC
Do đó A, D, E cùng thuộc đường trung trực của BC
Vậy A, D, E thẳng hàng
NH
1
H
10 tháng 4 2018
bn tự vẽ hình nha
Xét tam giác ABC cân tại A
\(\Rightarrow\)AB = AC
\(\Rightarrow\)A thuộc trung trực của BC (1)
Xét tam giác DBC cân tại D
\(\Rightarrow\)DB = DC
\(\Rightarrow\)D thuộc đường trung trực của BC (2)
xét ta giác EBC cân tại E
\(\Rightarrow\)EB = EC
\(\Rightarrow\)E thuộc đường trung trực của BC (3)
Từ (1) (2) (3):
\(\Rightarrow\)A , D , E thẳng hàng
~~ hok tốt ~~
19 tháng 4 2015
tam giác ABC ; DBC ; EBC lần lượt cân tại đỉnh A; D; E
=> AB = AC => A thuộc đường trung trưc của đoạn thẳng BC
DB = DC => D thuộc đường trung trực của đoạn thẳng BC
EB = EC => E thuộc đường trung trực của đoạn thẳng BC
Vậy A; D; E đều thuộc đường trung trực của đoạn thẳng BC hay A; D; E thẳng hàng
19 tháng 4 2017
Hướng dẫn:
Vì ∆ABC cân tại A => AB = AC
=> A thuộc trung trực của BC
Vì ∆DBC cân tại D => DB = DC
=> D thuộc trung trực của BC
Vì ∆EBC cân tại E => EB = EC
=> E thuộc trung trực của BC
Do đó A, D, E thuộc đường trung trực của BC nên A, D, E thẳng hàng
19 tháng 4 2017
Hướng dẫn:
Vì ∆ABC cân tại A => AB = AC
=> A thuộc trung trực của BC
Vì ∆DBC cân tại D => DB = DC
=> D thuộc trung trực của BC
Vì ∆EBC cân tại E => EB = EC
=> E thuộc trung trực của BC
Do đó A, D, E thuộc đường trung trực của BC nên A, D, E thẳng hàng
24 tháng 5 2020
(mạng cx đã có phần gợi ý, vc còn lại là lắp vào bài thôi.)
Xét \(\Delta\)ABC cân tại A ta có :
AB = AC
=> A thuộc đường trung trức của BC (1)
Xét \(\Delta\)DBC cân tại D ta có
DB = DC
=> D thuộc đường trung trực của BC (2)
Xét \(\Delta\)EBC cân tại E ta có :
EB = EC
=> E thuộc đường trung trực của BC (3)
Từ (1) ; (2) và (3)
Suy ra : A ; D ; E thuộc đường trung trực BC
và A ; D ; E thẳng hàng
Nguồn (gợi ý): Bài 46 SGK - tập 2 trang 76 - Toán lớp 7 | Học trực tuyến (vào TK nhìn thấy)
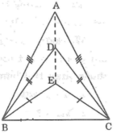
A B C D E
Vì AB = AC (gt) => A nằm trên đường trung trực của BC
Vì BD = DC (gt) => D nằm trên đường trung trực của BC
Vì BE = EC (gt) => E nằm trên đường trung trực của BC
=> A; D; E cùng nằm trên đường trung trực của BC
=> A ; D ; E thẳng hằng