tìm abcd biết ab * 3 = cd + 17
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
0
4 tháng 7 2019
Ta có:
cd - ab = 24
=> 3(cd - ab) = 24.3
=> 3cd - 3ab = 72
=> 3cd - cd = 72
=> (3 - 1).cd = 72
=> 2cd = 72
=> cd = 72 : 2 = 36
=> ab = cd : 3 = 36 : 3 = 12
=> abcd = 1236
4 tháng 7 2019
Cách khác
Thay \(\overline{ab}.3=\overline{cd}\)vào \(\overline{cd}-\overline{ab}=24\),ta được:
\(3\overline{ab}-\overline{ab}=24\)
\(\Rightarrow2\overline{ab}=24\)
\(\Rightarrow\overline{ab}=12\)
mà \(\overline{ab}.3=\overline{cd}\Rightarrow\overline{cd}=3.12=36\)
Vậy \(\overline{abcd}=1236\)
CM
1 tháng 11 2017
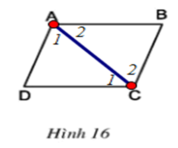
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)
Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)
Xét ΔABC và ΔCDA có:
∠A2 = ∠C1 (cmt)
AC chung
∠A1 = ∠C2 (cmt)
⇒ ΔABC = ΔCDA (g.c.g)
⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)
b)
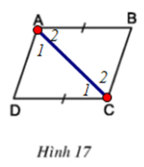
Xét ΔABC và ΔCDA có:
AC chung
∠A2 = ∠C1 (cmt)
AB = CD
⇒ ΔABC = ΔCDA (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)
NT
0
NM
1
LB
20 tháng 8 2017
Xét tam giác vuông \(AHC\)và tam giác vuông \(BKD\)ta có:
\(AD=BC\left(gt\right)\)
\(\widehat{C}=\widehat{D}\left(gt\right)\)
\(\Rightarrow\)tam giác vuông AHD = tam giác vuông BKC ( cạnh huyền - góc nhọn )
=> HC=HD(2 cạnh tương ứng)
Ta có: \(HK=10cm\)
\(\Rightarrow HC=\frac{CD-HK}{2}=\frac{26-10}{2}=8cm\)
Áp dụng định lí Pytago trong tam giác vuông AHC:
\(AC^2=HC^2+AH^2\\ \Rightarrow AH^2=AC^2-HC^2\\ =289-64=225\\ \Rightarrow AH=\sqrt{225}=15cm\)
Vậy đường cao của hình thang ABCD là 15cm
PV
4
7 tháng 8 2017
cdab - abcd = 4356
(cd x 100 + ab) - (ab x 100 + cd) = 4356
cd x 100 + ab - ab x 100 - cd = 4356
cd x 99 + ab - ab x 100 = 4356
cd x 99 - ab x 99 = 4356
(cd - ab) x 99 = 4356
(cd - ab) = 4356 : 99 = 44
ab là:
(92 - 44) : 2 = 24
cd là:
92 - 24 = 68
BT
7 tháng 8 2017
cdab-abcd=4356
<=> 100cd+ab-(100ab+cd)=4356
<=> 100cd+ab-100ab-cd=4356
<=> 99.cd - 99.ab=4356
<=> cd-ab=44
Lại có: cd+ab=92
=> cd=\(\frac{44+92}{2}=68\)
ab=68-44=24
Đáp số: ab=24; cd=68