Tìm x,y\(\in Z\): xy2+2xy+x=32y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 2 2017
pt <=> \(x\left(y^2+2y+1\right)=32y\)
\(\Leftrightarrow x\left(y+1\right)^2=32y\)
\(\Leftrightarrow\frac{x}{y}.\left(y+1\right)^2=32\)
do x,y \(\in\)N* => y+1>1
\(\Leftrightarrow\frac{x}{y}.\left(y+1\right)^2=2.4^2=8.2^2\)
TH1: \(\hept{\begin{cases}\frac{x}{y}=2\\y+1=4\end{cases}\Leftrightarrow}\hept{\begin{cases}x=6\\y=3\end{cases}}\)
TH2: \(\hept{\begin{cases}\frac{x}{y}=8\\y+1=2\end{cases}\Leftrightarrow}\hept{\begin{cases}x=8\\y=1\end{cases}}\)
Vậy (x,y)=...
AH
Akai Haruma
Giáo viên
13 tháng 10 2018
Lời giải:
\(xy^2+2xy+x=32y\)
\(\Leftrightarrow x(y^2+2y+1)=32y\)
\(\Leftrightarrow x(y+1)^2=32y\Rightarrow x=\frac{32y}{(y+1)^2}\)
Ta thấy \((y+1)^2-4y=(y-1)^2\geq 0\Rightarrow (y+1)^2\geq 4y\)
\(\Rightarrow x=\frac{32y}{(y+1)^2}\leq \frac{32y}{4y}=8\)
Từ đây ta xét các TH:
+) Nếu $x$ chẵn thì \(x\in\left\{2;4;6;8\right\}\)
Thử từng giá trị của $x$ ta thu được \((x,y)=(6,3); (8,1)\)
+) Nếu $x$ lẻ thì vì \(x(y+1)^2=32y\vdots 32\Rightarrow (y+1)^2\vdots 32\)
\(y+1\vdots 8\)
\(\Rightarrow 32y=x(y+1)^2\vdots 64\Rightarrow y\vdots 2\) (vô lý vì $y+1$ chẵn thì $y$ phải lẻ)
Vậy $(x,y)=(6,3), (8,1)$
20 tháng 8 2021
a: Thay x=1; y=-1 và z=-2 vào biểu thức \(2xy\left(5x^2y+3x-z\right)\), ta được:
\(2\cdot1\cdot\left(-1\right)\cdot\left(-5+3+2\right)\)
=0
b: Thay x=1; y=-1 và z=-2 vào biểu thức \(xy^2+y^2z^3+z^3x^4\), ta được:
\(1\cdot\left(-1\right)^2+\left(-1\right)^2\cdot\left(-8\right)+\left(-8\right)\cdot1\)
\(=1-8-8=-15\)
TN
1
25 tháng 10 2019
\(xy^2+2xy+x=32y\)
\(x\left(y+1\right)^2=32y\)
\(\Rightarrow x=\frac{32y}{\left(y+1\right)^2}\)
Vì \(\left(y,\left(y+1\right)^2\right)=1\)và \(x\inℤ\)\(\Rightarrow\left(y+1\right)^2\inƯ\left(32\right)=Ư\left(2^5\right)=\left\{2^2;2^4\right\}\)
\(Khi\left(y+1\right)^2=2^2=4\Rightarrow\orbr{\begin{cases}y+1=2\\y+1=-2\end{cases}}\Leftrightarrow\orbr{\begin{cases}y=1\\y=-3\end{cases}}\)
\(\cdot y=1\Rightarrow x=\frac{32.1}{4}=8\)
\(\cdot y=-3\Rightarrow x=\frac{32.\left(-3\right)}{4}=-24\)
\(Khi\left(y+1\right)^2=2^4=16\Rightarrow\orbr{\begin{cases}y+1=4\\y+1=-4\end{cases}\Leftrightarrow\orbr{\begin{cases}y=3\\y=-5\end{cases}}}\)
\(\cdot y=3\Rightarrow x=\frac{32.3}{16}=6\)
\(\cdot y=-5\Rightarrow x=\frac{32.\left(-5\right)}{16}=-10\)
Vậy nghiệm phương trình \(\left(x;y\right)=\left(8;1\right);\left(-24;-3\right);\left(6;3\right);\left(-10;-5\right)\)
TC
3
VT
16 tháng 6 2017
X(y3 + 2y + 1) = 32y
Vì (y3 + 2y + 1; y) = 1 nen 32 \(⋮\)chia hết cho y3 + 2y + 1.
Đến đây tự giải nhé.
TC
17 tháng 6 2017
ủa bạn cái đoạn \(\left(y^3+2y+1;y\right)=1\) dấu chấm phẩy “;” nghĩa là sao ?
NM
0
28 tháng 3 2018
a) Thay x = 1 ; y = –1 và z = –2 vào biểu thức ta được:
2xy(5x2y + 3x – z) = 2.1(–1).[5.12.(–1) + 3.1 – (–2)]
= -2[–5 + 3 +2] = –2.0 = 0
Vậy đa thức có giá trị bằng 0 tại x = 1 ; y = –1 và z = –2.
b) Thay x = 1 ; y = –1 và z = –2 vào biểu thức ta được:
xy2 + y2z3 + z3x4 = 1.(–1)2 + (–1)2(–2)3 + (–2)314
= 1 + (–8) + (–8) = –15
Vậy đa thức có giá trị bằng -15 tại x = 1 ; y = –1 và z = –2.
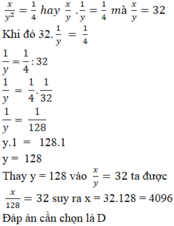
xy2 + 2xy + x = 32y
xy2 + 2xy - 32y + x = 0
<=> x = 32y/ ( y2 + 2y + 1) = 32/ (y + 1) - 32/( y + 1)2
x nguyên khi (y+1)^2 là ước của 32 => (y+1)^2 = 1,4,16
=> y + 1 = 1,2,4 vì y nguyên dương
=>y = 0( loại ) ; 1;3
=> x