tích của 2 số là 7500 biết S1=3/4 S2.Tìm S2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D.
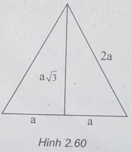
(h.2.60) Bán kính đáy của hình nón là a, đường sinh của hình nón là 2a.
Do đó, ta có:
S 1 = π Rl = π .a.2a = 2 πa 2 (1)
Mặt cầu có bán kính là a 3 /2, nên ta có:
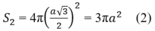
Từ (1) và (2) suy ra: 2 S 2 = 3 S 1

Bài 2:
$S_1=1+[(-3)+5]+[(-7)+9]+...+[(-15)+17]$
$=1+2+2+....+2$
Số lần xuất hiện của 2 là: $[(17-3):2+1]:2=4$
$\Rightarrow S_1=1+2.4=9$
-------------------------
$S_2=(-2)+[4+(-6)]+[8+(-10)]+...+[16+(-18)]$
$=(-2)+(-2)+(-2)+...+(-2)$
Số lần xuất hiện của -2 là:
$[(18-4):2+1]:2+1=5$
$\Rightarrow S_2=(-2).5=-10$
$S_1+S_2=9+(-10)=-1$

\(S_{\left(S_1\right)}=4\pi R_1^2\)
\(S_{\left(S_2\right)}=4\pi R_2^2=4\pi\left(2R_1\right)^2=4.4\pi R_1^2\)
\(\Rightarrow\dfrac{S_{\left(S_2\right)}}{S_{\left(S_1\right)}}=4\)


Ta thấy tam giác ADC và tam giác ABC có chung chiều cao hạ từ đỉnh C nên \(\frac{S_{ADC}}{S_{ABC}}=\frac{AD}{AB}\)
Ta thấy tam giác BEC và tam giác BAC có chung chiều cao hạ từ đỉnh B nên \(\frac{S_{BEC}}{S_{BAC}}=\frac{CE}{AC}\)
Lại có AD = CE, AB = AC nên \(\frac{S_{ADC}}{S_{ABC}}=\frac{S_{BEC}}{S_{BAC}}\Rightarrow S_{ADC}=S_{BEC}\)
\(\Rightarrow S_{ADC}-S_{MEC}=S_{BEC}-S_{MEC}\Rightarrow S_{ADME}=S_{BMC}\Rightarrow S_1=S_2\)
Từ đó ta có: \(\frac{S_1}{S_2\times2+S_1\times3}=\frac{S_1}{S_1\times2+S_1\times3}=\frac{S_1}{S_1\times5}=\frac{1}{5}\)
Bài giải :

Ta thấy tam giác ADC và tam giác ABC có chung chiều cao hạ từ đỉnh C nên SADCSABC =ADAB
Ta thấy tam giác BEC và tam giác BAC có chung chiều cao hạ từ đỉnh B nên SBECSBAC =CEAC
Lại có AD = CE, AB = AC nên SADCSABC =SBECSBAC ⇒SADC=SBEC
⇒SADC−SMEC=SBEC−SMEC⇒SADME=SBMC⇒S1=S2
Từ đó ta có: S1S2×2+S1×3 =S1S1×2+S1×3 =S1S1×5 =15




100 nha ban
2/2x4+2/4x6+2/6x8+................2/2014x2016