chứng tỏ rằng 1/2^2 + 1/3^2 +...+1/100^2 <1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
0
SM
0
NK
2
XO
3 tháng 6 2019
Ta có : \(\frac{1}{2}+\frac{2}{3}+..+\frac{99}{100}\)
= \((1-\frac{1}{2})+(1-\frac{1}{3})+...+(1-\frac{99}{100})\)(100 cặp số )
= \(\left(1+1+1+...+1\right)-\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{100}\right)\)(100 số hạng 1)
= \(1\times100-\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+..+\frac{1}{100}\right)\)
= \(100-\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{100}\right)\)
=> 100-(1+1/2+1/3+...+1/100) = 1/2+2/3+3/4+...+99/100
LV
0
NT
2
VT
22 tháng 4 2015
Co 1/2^2+1/3^2+...+1/100^2<1/1.2+1/2.3+...+1/99.100
=1-1/2+1/2-1/3+...+1/99-1/100
=1-1/100<1
vay 1/2^2+...+1/100^2<1
22 tháng 4 2015
Ta thấy: \(\frac{1}{2^2}<\frac{1}{1.2};\frac{1}{3^2}<\frac{1}{2.3};....;\frac{1}{100^2}<\frac{1}{99.100}\)
Cộng vế theo vế ta được: \(\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{100^2}<\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{99.100}\)
Mà \(\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{98.99}+\frac{1}{99.100}=\left(1-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+...+\left(\frac{1}{98}-\frac{1}{99}\right)+\left(\frac{1}{99}-\frac{1}{100}\right)\) \(=1-\frac{1}{100}<1\)
Do đó: \(\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{100^2}<\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{99.100}<1\)
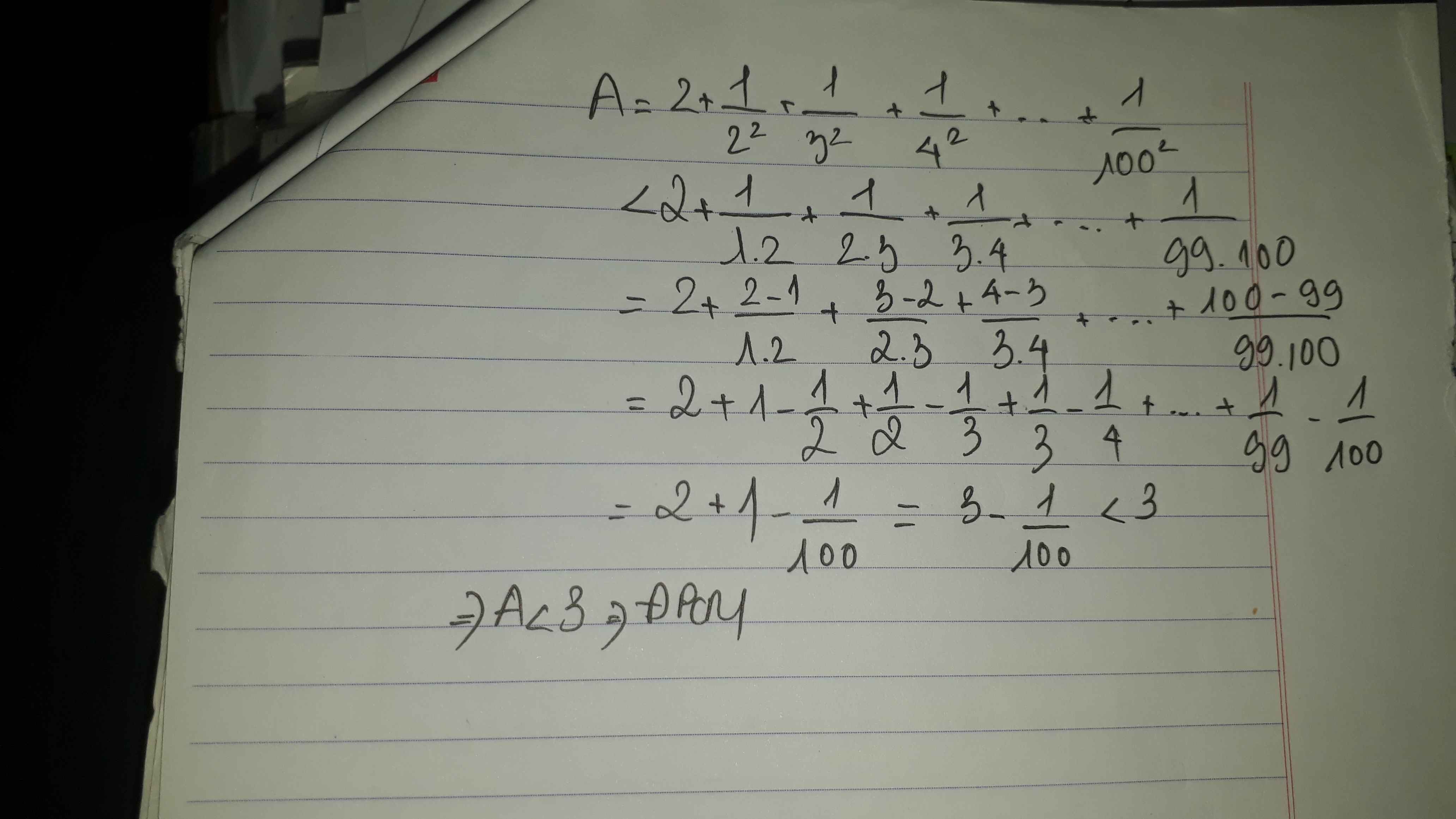
\(\frac{1}{2^2}< \frac{1}{1.2};\frac{1}{3^2}< \frac{1}{2.3};...;\frac{1}{100^2}< \frac{1}{99.100}\)
Cộng vế với vế ta được :
\(\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{100^2}< \frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{99.100}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{99}-\frac{1}{100}=1-\frac{1}{100}=\frac{99}{100}< 1\)
Vậy ta có đpcm