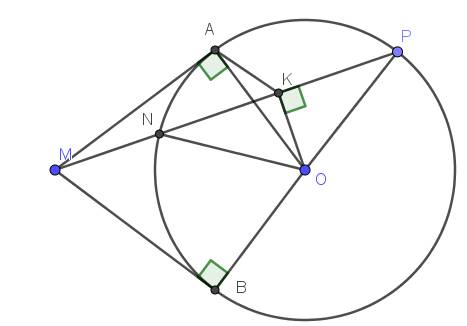
Từ điểm A ở ngoài đường tròn (O

NH

Nguyễn Hoàng Tiến

20 tháng 2 2017 - olm

Từ điểm A ở ngoài đường tròn (O;R) dựng các tiếp tuyến AB, AC và cát tuyến ADE (D,E thuộc (O) và D nằm giữa A,E). Đường thẳng qua D vuông góc với OB cắt BC, BE lần lượt tại H và K. Vẽ OI vuông góc với AE tại I.a) Chứng minh rằng tứ giác OIBC nội tiếp được đường tròn. (đã xong)b) Chứng minh rằng IA là tia phân giác góc BIC. (đã xong)c) Gọi S là giao điểm của BC và AD. Chứng minh rằng 2/AS...

Đọc tiếp

#Toán lớp 9

0

PT

Phan Thị Hà Vy

14 tháng 8 2018 - olm

cho đường tròn (O;R) và đường thẳng a ở ngoài đường thẳng a ở ngoài đường tròn. Gọi OH là khoảng cách từ tâm O đếna và M là một điểm chuyển động trên a. Từ M kẻ hai tiếp tuyến MA,MB với đường tròn (O) , (A,B là 2 tiếp điểm). Gọi D là giao điểm của AB với OH.CMR D là điểm cố định

#Toán lớp 9

3

NT

Nguyễn Tũn

14 tháng 8 2018

dễ ẹc!!!!!!!!

Đúng(0)

HN

Hn . never die !

1 tháng 5 2020

Trả lời :

Bn Nguyễn Tũn bảo dễ ẹt thì làm đi.

- Hok tốt !

^_^

Đúng(0)

HT

Hoàng Thị Thu Hương

24 tháng 3 2022

Cho đường tròn O từ điểm A bên ngoài đường tròn, kẽ tiếp tuyến AB, AC đường thẳng qua C // AB cắt đường tròn ở D, AD cắt đường tròn O ở M, CM cắt AB ở N a, góc BAD = góc ACN b, AN2 = NM* NC

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

27 tháng 7 2023

a: góc ACN=1/2*sđ cung MC

góc BAD=góc MDC=1/2*sđ cung MC

=>góc ACN=góc BAD

b: Xét ΔNAM và ΔNCA có

góc NAM=góc NCA

góc N chung

=>ΔNAM đồng dạng với ΔNCA

=>NA/NC=NM/NA

=>NA^2=NM*NC

Đúng(0)

PT

Phát Thuận

25 tháng 4 2022

Từ một điểm a ở bên ngoài đường tròn tâm O,kẻ hai tiếp tuyến AB,AC với đường tròn này

#Toán lớp 9

1

NQ

Nguyễn Quang Minh

25 tháng 4 2022

Đúng(0)

YA

You are my sunshine

25 tháng 4 2022

ukm ukm nhưng điểm đâu :)

Đúng(1)

KL

Kiều Lam

31 tháng 3 2021

cho đường tròn(o;r), từ điểm a ở bên ngoài đường tròn kẻ 2 tiếp tuyến ab, ac với đường tròn(o) (b,c là tiếp điểm) từ b kẻ đường thẳng song song ac cắt đường tròn(o) tại d(d khác b), đường thẳng ad cắt đường tròn (o) tại e( e khác d) a) chứng minh tứ giác aboc nội tiếp b) chứng minh ab²= ae×ad c) giả sử oa=2r. Tính góc bec và diện tích obac d) so sánh góc cea và góc bec

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

31 tháng 3 2021

a) Xét tứ giác ABOC có

$\widehat{ABO}$ và $\widehat{ACO}$ là hai góc đối

$\widehat{ABO}+\widehat{ACO}=180^0\left(90^0+90^0=180^0\right)$

Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Đúng(1)

DT

đỗ tuệ minh

21 tháng 12 2021

Cho đường tròn (O). Từ điểm A bên ngoài đường tròn vẽ 2 tiếp tuyến AB ,AC với đường tròn (B,C là các tiếp điểm).Đường thẳng kẻ qua C song song với AB cắt đường tròn (O) ở D ,AD cắt (O) ở M ,CM cắt AB ở N. Chứng minh:a) Góc BAD=góc ACNb)$^{AN^{ }2}$=NM.NCC)N là trung điểm của...

Đọc tiếp

#Tin học lớp 9

0

3T

30.Nɠυұễɳ Tɦàɲɦ Pɦúƈ ヅ

8 tháng 12 2023

Từ điểm A ở bên ngoài đường tròn (O), kẻ 2 tiếp tuyến AB và AC đến đường tròn (O) (B, C là tiếp điểm). Kẻ cát tuyến ADE vs đường tròn (O) (D nằm giữa A và E).a) Cm: 4 điểm A, B, O, C cùng thuộc một đường trònb) Cm OA ⊥ BC tại H và OD² = OH × OA. Từ đó suy ra tam giác OHD đồng dạng vs tam giác ODA. Giải và vẽ hình giúp mình vớiii !!...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

8 tháng 12 2023

a: Xét tứ giác ABOC có

$\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0$

=>ABOC là tứ giác nội tiếp

=>A,B,C,O cùng thuộc một đường tròn

b: Xét (O) có

AB,AC là tiếp tuyến

Do đó: AB=AC

=>A nằm trên đường trung trực của BC(1)

Ta có: OB=OC

=>O nằm trên đường trung trực của BC(2)

Từ (1) và (2) suy ra OA là đường trung trực của BC

=>OA$\perp$BC tại H và H là trung điểm của BC

Xét ΔOBA vuông tại B có BH là đường cao

nên $OH\cdot OA=OB^2$

mà OB=OD

nên $OD^2=OH\cdot OA$

=>$\dfrac{OD}{OH}=\dfrac{OA}{OD}$

Xét ΔODA và ΔOHD có

$\dfrac{OD}{OH}=\dfrac{OA}{OD}$

$\widehat{DOA}$ chung

Do đó: ΔODA đồng dạng với ΔOHD

Đúng(1)

3T

30.Nɠυұễɳ Tɦàɲɦ Pɦúƈ ヅ

9 tháng 12 2023

Từ điểm A ở ngoài đường tròn (O), kẻ 2 tiếp tuyến AB, AC đến đường tròn (O) (B, C là tiếp điểm). Kẻ cát tuyến ADE với đường tròn (O) (D nằm giữa A và E).a) Cm: 4 điểm A, B, O, C cùng thuộc một đường trònb) Cm OA ⊥ BC tại H và OD² = OH × OA. Từ đó suy ra tam giác OHD đồng dạng với tam giác ODA.--> Cần hình vẽ ạ! (Bài giải e làm...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

9 tháng 12 2023

loading...

Đúng(1)

N

NguyenBaoKhanh

15 tháng 11 2023 - olm

Từ điểm M ở ngoài đường tròn (O; R) kẻ hai tiếp tuyến MA, MB và cát tuyến MNP tới
đường tròn (O); gọi K là trung điểm của NP. Chứng minh rằng: 5 điểm M, A, O, K, B cùng thuộc
1 đường tròn

#Toán lớp 9

1

AH

Akai Haruma

Giáo viên

18 tháng 11 2023

Lời giải:

Vì $MA,MB$ là tiếp tuyến của $O$ nên $MA\perp OA, MB\perp OB$

$\Rightarrow \widehat{MAO}=\widehat{MBO}=90^0$

Xét tứ giác $MAOB$ có $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$. Mà 2 góc này đối nhau nên $MAOB$ là tứ giác nội tiếp.

$\Rightarrow M, A,O,B$ cùng thuộc 1 đường tròn (1)

Mặt khác:

Tam giác $ONP$ cân tại $O$ (do $ON=OP=R$) nên trung tuyến $OK$ đồng thời là đường cao.

$\Rightarrow \widehat{MKO}=90^0$

Xét tứ giác $MAKO$ có $\widehat{MAO}=\widehat{MKO}=90^0$. Mà 2 góc này cùng nhìn cạnh $MO$ nên $MAKO$ là tứ giác nội tiếp.

$\Rightarrow M,A,K,O$ cùng thuộc 1 đường tròn (2)

Từ $(1); (2)\Rightarrow M, A, O, K,B$ cùng thuộc 1 đường tròn.

Đúng(0)

N

NguyenBaoKhanh

15 tháng 11 2023 - olm

Từ điểm M ở ngoài đường tròn (O; R) kẻ hai tiếp tuyến MA, MB và cát tuyến MNP tới
đường tròn (O); gọi K là trung điểm của NP. Chứng minh rằng: 5 điểm M, A, O, K, B cùng thuộc
1 đường tròn

#Toán lớp 9

2

AH

Akai Haruma

Giáo viên

18 tháng 11 2023

Lời giải:

Vì $MA,MB$ là tiếp tuyến của $O$ nên $MA\perp OA, MB\perp OB$

$\Rightarrow \widehat{MAO}=\widehat{MBO}=90^0$

Xét tứ giác $MAOB$ có $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$. Mà 2 góc này đối nhau nên $MAOB$ là tứ giác nội tiếp.

$\Rightarrow M, A,O,B$ cùng thuộc 1 đường tròn (1)

Mặt khác:

Tam giác $ONP$ cân tại $O$ (do $ON=OP=R$) nên trung tuyến $OK$ đồng thời là đường cao.

$\Rightarrow \widehat{MKO}=90^0$

Xét tứ giác $MAKO$ có $\widehat{MAO}=\widehat{MKO}=90^0$. Mà 2 góc này cùng nhìn cạnh $MO$ nên $MAKO$ là tứ giác nội tiếp.

$\Rightarrow M,A,K,O$ cùng thuộc 1 đường tròn (2)

Từ $(1); (2)\Rightarrow M, A, O, K,B$ cùng thuộc 1 đường tròn.

Đúng(1)

AH

Akai Haruma

Giáo viên

18 tháng 11 2023

Hình vẽ:

Đúng(1)

DV

Đỗ Vũ Thảo Nhi

25 tháng 11 2023

Bài 6: (2,5 điểm) Từ điểm A ở ngoài đường tròn (O; R) kẻ tiếp tuyến AB (B là tiếp điểm). Kẻ đường kính BC của đường tròn (O). Đoạn AC cắt đường tròn (O) tại điểm D (khác C). a) Chứng minh tam giác BDC vuông và . AC = A * B ^ 2 = A * O ^ 2 - R ^ 2 b) Qua B kẻ đường thẳng d vuông góc với AO tại H. Đường thẳng d cắt đường tròn (O) tại E (khác B). Gọi F là điểm đối xứng của H qua O. Chứng...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

25 tháng 11 2023

a:

Sửa đề: $AD\cdot AC=AB^2=AO^2-R^2$

Xét (O) có

ΔBDC nội tiếp

BC là đường kính

Do đó: ΔBDC vuông tại D

=>BD$\perp$DC tại D

=>BD$\perp$CA tại D

Xét ΔBCA vuông tại B có BD là đường cao

nên $AD\cdot AC=AB^2\left(1\right)$

Xét ΔOBA vuông tại B có $OB^2+BA^2=OA^2$

=>$BA^2+R^2=OA^2$

=>$BA^2=OA^2-R^2\left(2\right)$

Từ (1) và (2) suy ra $AD\cdot AC=AB^2=OA^2-R^2$

b: ΔOBE cân tại O

mà OH là đường cao

nên H là trung điểm của BE

Xét ΔBCE có

O,H lần lượt là trung điểm của BC,BE

=>OH là đường trung bình của ΔBCE

=>OH//CE và OH=1/2CE

OH//CE

F$\in$OH

Do đó: HF//CE

$OH=\dfrac{1}{2}CE$

$OH=\dfrac{1}{2}FH$

Do đó: CE=FH

Xét tứ giác CEHF có

CE//HF

CE=HF

Do đó: CEHF là hình bình hành

Hình bình hành CEHF có $\widehat{FHE}=90^0$

nên CEHF là hình chữ nhật

ΔOBE cân tại O

mà OH là đường cao

nên OH là phân giác của góc BOE

Xét ΔOBA và ΔOEA có

OB=OE

$\widehat{BOA}=\widehat{EOA}$

OA chung

Do đó: ΔOBA=ΔOEA

=>$\widehat{OBA}=\widehat{OEA}=90^0$

=>AE là tiếp tuyến của (O)

c: Xét (O) có

ΔBGC nội tiếp

BC là đường kính

Do đó: ΔBGC vuông tại G

=>GB$\perp$GC tại G

Xét ΔHEC vuông tại E và ΔHGB vuông tại G có

$\widehat{EHC}=\widehat{GHB}$

Do đó: ΔHEC đồng dạng với ΔHGB

=>$\dfrac{HE}{HG}=\dfrac{HC}{HB}$

=>$HE\cdot HB=HG\cdot HC$

=>$HG\cdot HC=HB^2\left(3\right)$

Xét ΔBOA vuông tại B có BH là đường cao

nên $HO\cdot HA=HB^2\left(4\right)$

Từ (3) và (4) suy ra $HG\cdot HC=HO\cdot HA$

Đúng(1)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP