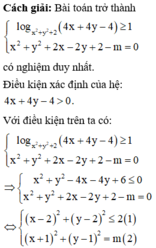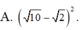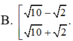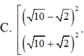Tìm tất cả các giá trị của x, y thỏa mãn đẳng thức: y2 + 2y + yx - 2x + 1 + 2 = 0.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a\text{) }pt\Leftrightarrow\left(y^2+2y+1\right)+\left[\left(2^x\right)^2-2.2^x+1\right]=0\)
\(\Leftrightarrow\left(y+1\right)^2+\left(2^x-1\right)^2=0\)
\(\Leftrightarrow y+1=0\text{ và }2^x-1=0\)
\(\Leftrightarrow y=-1\text{ và }x=0\)
\(b\text{) }pt\Leftrightarrow\left(4x^2+4y^2+8xy\right)+\left(x^2-2x+1\right)+\left(y^2+2y+1\right)=0\)
\(\Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
\(\Leftrightarrow x+y=0\text{ và }x-1=0\text{ và }y+1=0\)
\(\Leftrightarrow x=1\text{ và }y=-1\)

Đáp án A
Ta có, giả thiết
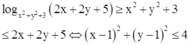
là miền trong đường tròn tâm I(1;1) bán kính R1 = 2
Và


\(5x^2+5y^2+8xy-2x+2y+2=0\)
=>\(4x^2+8xy+4y^2+x^2-2x+1+y^2+2y+1=0\)
=>\(4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
=>x=1 và y=-1
\(M=\left(1-1\right)^{2023}+\left(1-2\right)^{2024}+\left(-1+1\right)^{2025}=1\)

Sửa đề: \(5x^2+5y^2+8xy-2x+2y+2=0\)
=>\(4x^2+8xy+4y^2+x^2-2x+1+y^2+2y+1=0\)
=>\(\left(2x+2y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
=>\(\left\{{}\begin{matrix}2x+2y=0\\x-1=0\\y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(M=\left(x-y\right)^{2023}-\left(x-2\right)^{2024}+\left(y+1\right)^{2023}\)
\(=\left(1+1\right)^{2023}-\left(1-2\right)^{2024}+\left(-1+1\right)^{2023}\)
\(=2^{2023}-1\)

Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.