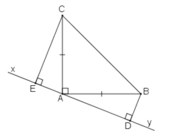
cho tam giac ABC vuông tại A có AB = AC.Qua A vẽ đường thẳng xy (B,C cùng phía đối với xy).Kẻ BD và CE vuông góc với xy ( D,E thuộc xy).Khi đó\(\frac{BD}{ED}+\frac{CE}{DE}=\)
Giups mk nha các bn!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DV
8 tháng 12 2016
Bạn tự vẽ hình giùm mình nhé!
a) Xét tam giác BAD và tam giác ACE có:
AB = AC (gt)
BDA = CEA =1V
DBA = EAC (vì cùng phụ với DAB)
Nên tam giác BAD = tam giác ACE (chgn)
b) Từ c/m a, có: tam giác BAD bằng tam giác ACE => AD=EC; AE=DB
=> DE = DA + AE= EC+BD (đpcm)
1 tháng 9 2018
a) Xét tam giác BAD và tam giác ACE có : AB = AC (gt)
BDA = CEA = 90o
Góc DBA = Góc EAC (vì cùng phụ với DAB)
Vậy tam giác BAD = tam giác ACE (ch - gn)
CM
29 tháng 9 2018
Ta có: ΔAEC= ΔBDA
⇒AE = BD và EC = DA
Mà DE = DA + AE
Vậy: DE = CE + BD
11 tháng 6 2017
a) Xét ∆BAD và ∆ACE có:
^BDA=^AEC (cùng bằng 90 độ)
AB=AC (gt)
^BAD=^ACE (cùng phụ với ^EAC)
suy ra ∆BAD=∆ACE (cạnh huyền-góc nhọn)
b) Do ∆BAD=∆ACE nên AD=CE và AE=BD
mà DE=DA+AE
suy ra DE = CE+BD (đpcm)
Bài 2)
a) Xét ∆AOD và ∆COB có:
^OAD=^OCB(so le trong)
AD=BC(gt)
^ADO=^CBO(so le trong)
suy ra ∆AOD=∆COB (g-c-g)
do đó OA=OC (hai cạnh tương tứng)
b)
Xét ∆AEO và ∆COF có:
^EAO=^OCF (so le trong)
OA=OC (c/m trên)
^AOE=^COF (đối đỉnh)
suy ra ∆AEO=∆COF (g-c-g)
do đó OE=OF (hai cạnh tương ứng)
26 tháng 4
a) Vì góc BAC = 90 độ(gt)
suy ra : Góc A1 + góc A2 = 90 độ (1)
Xét tam giác ACE , có :
góc A + góc C + góc E = 180 độ ( Áp dụng tổng 3 góc trong một tam giác )
hay góc A + góc C + 90 độ = 180 độ
suy ra : góc A + góc C =180 độ - 90 độ
suy ra : góc A + góc C = 90 độ (2)
Từ (1) và (2) , suy ra :
Góc A1 = góc C1 (ĐPCM)
b) Xét tam giác ABD và tam giác ACE . Có :
Góc A1 = Góc C1 (CMT)
AB = AC ( gt)
Góc ADB = Góc AEC ( vì cùng bằng 90 độ )
Suy ra : Tam giác ABD = Tam giác ACE ( cạnh huyền - góc nhọn ) (ĐPCM)
c) Xét tam giác ABD vuông tại D và tam giác ACE vuông tại E . Có :
AB=AC(gt)
suy ra : BD = CE (1)
Mà : BD vuông góc với xy tại D (gt)(2)
CE vuông góc với xy tại E (gt)(3)
Từ (1), (2) và (3) . Suy ra :
DE = BD+CE ( ĐPCM)
26 tháng 4
hình thì các bạn bên dưới hoặc bên trên đã vẽ đúng hết rồi nha