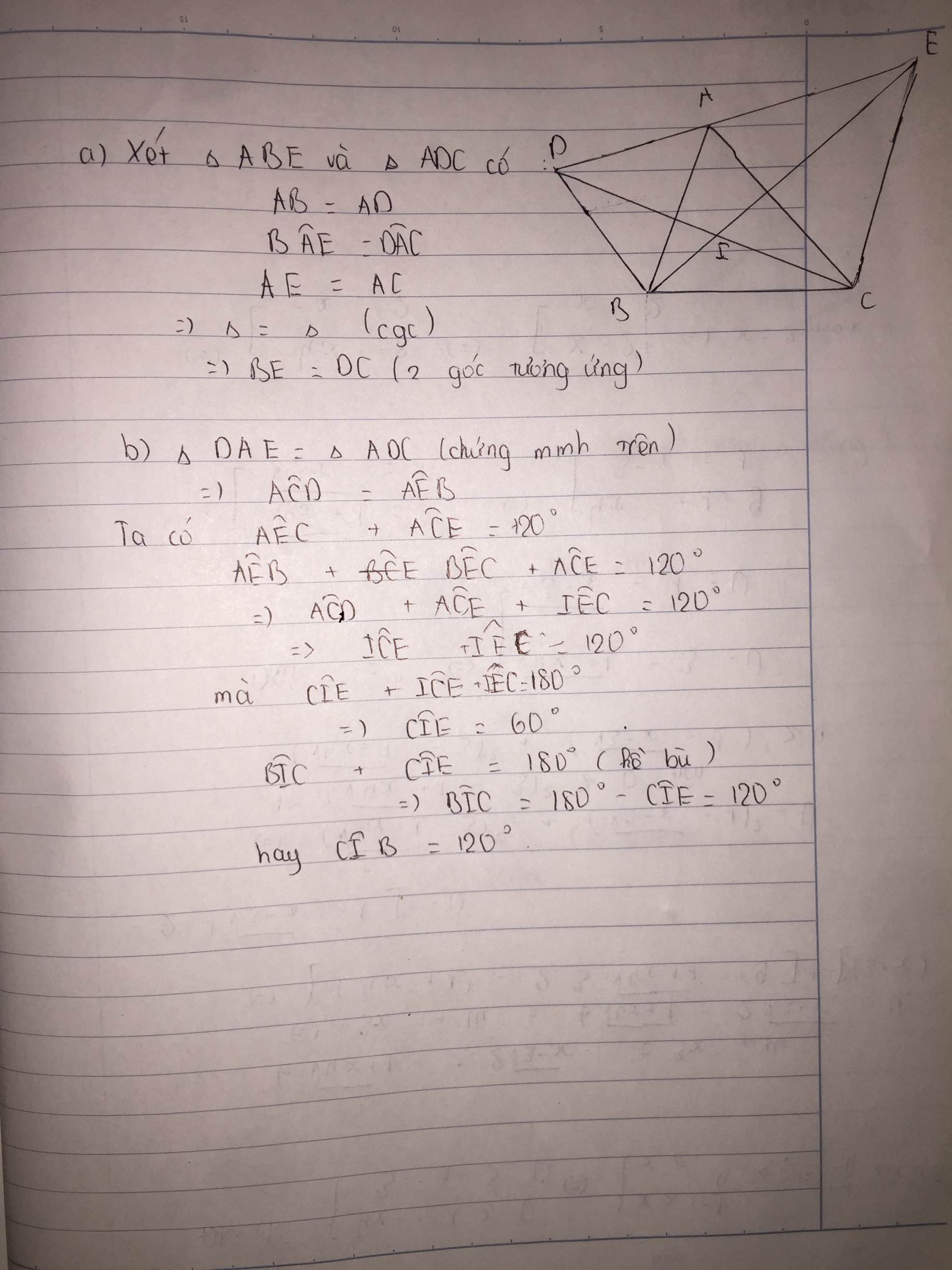Cho tam giác ABC có các góc nhọn < 120 độ. Ở phía ngoài tam giác ABC vẽ các tam giác đều ABD, ACE. a) Chứng minh DC=BE b) Gọi I là giao điểm của DC và BE. Tính góc BIC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 2 2022
Vì △ ABD đều ⇒ DAB= 60
△ACE đều ⇒ EAC = 60
⇒ DAB+ BAC= BAC+ EAC
⇒ DAC= BAE
Xét △ ABE và △ ADC có
AB= AD ( vì △ABD đều)
DAC=BAE (cmt)
AE= AC ( vì △ACE đều)
⇒ △ ABE = △ADC ( c.g.c)
⇒BE = DC (2 cạnh tương ứng)
Vậy ...
Nhớ tích cho mik nha
D
16 tháng 4 2017
Xét tam giác ADC và tam giác AEB có:
AD = AB(giả thiết)
\(\widehat{DAC}=\widehat{BAE}\)(\(=60^0+\widehat{BAC}\))
AC = AE( giả thiết)
\(\Rightarrow\)tam giác ADC = tam giác ABE (c-g-c)
\(\Rightarrow\widehat{ADC}=\widehat{ABE}\)(2 góc tương ứng)
Xét tam giác ADI và tam giác BIM có:
\(\widehat{ADI}+\widehat{AIM}+\widehat{DAI}=\widehat{IBM}+\widehat{BIM}+\widehat{IMB}=180^0\)(theo định lí tổng 3 góc của tam giác)
Mà \(\widehat{ADI}=\widehat{IBM}\)(chứng minh trên)
\(\widehat{AID}=\widehat{BIM}\)(2 góc đối đỉnh)
\(\Rightarrow\widehat{DAI}=\widehat{IMB}\)
Mà \(\widehat{DAI}=60^0\)
\(\Rightarrow\widehat{IMB}=60^0\)
Ta có: \(\widehat{IMB}+\widehat{BMC}=180^0\)(2 góc kề bù)
\(\Rightarrow60^0+\widehat{BMC}=180^0\)
\(\Rightarrow\widehat{BMC}=180^0-60^0=120^0\)
Vậy \(\widehat{BMC}=120^0\)(ĐPCM)
