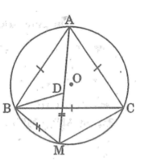
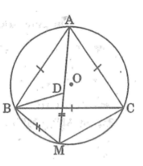
cho tam giác abc đều nội tiếp đường tròn (o) và 1 điểm D nằm trên cung BC.Trên DA lấy điểm E sao cho DE=DB.CM tam giác DBE đều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


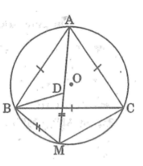
Ta có: ∆ ABD = ∆ CBM (cmt)
suy ra: AD = CM
Ta có: DM = BM ( tam giác MBD đều )
mà AM = AD + DM
suy ra: MA = MC + MB

Ta có:BD = DE (gt) \(\Rightarrow\Delta\)DBE cân tại D (1)
Ta lại có: \(\widehat{ADB}=\widehat{ACB}\) ( cùng chắn cung AB)
mà \(\widehat{ACB}\)=60 độ (\(\Delta\)ABC đều)
\(\Rightarrow\widehat{ADB}\)=60 độ \(\Rightarrow\widehat{EDB}\)=60 độ (E \(\in\) AD) (2)
Từ (1) và (2) \(\Rightarrow\Delta\)DEB đều

bạn ơi câu a ko có dữ liệu thì tính sao được còn câu b đợi mk tí mk làm cho
b) vì MD=MB ==> tam giác BDM cân tại M
mà góc BMD=góc ACB=60 độ
do đó tam giác BDM đều ==>DBM=60 độ
ta có ABD+DBC=60 độ
MBC+DBC=60 độ
==> góc ABD= CBM
DO ĐÓ TAM GIÁC ABD= tam giác CBM(c.g.c)
==> AD=CM ==> AD+DM=BM+MC=AM
==> ĐIỀU CẦN CHỨNG MINH