Cho f(x)=x2-3x-5, giá trị của \(k\)không âm để f(k)=k là.......
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có
\(f\left(x\right)=x^2-3x-5=x\Leftrightarrow x^2-4x+4=9\)\(\Leftrightarrow\left(x-2\right)^2=3^2\)\(\Leftrightarrow\orbr{\begin{cases}x-2=3\\x-2=-3\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=5\\x=-1\end{cases}}\)
Vậy x=... thì f(k)=k


f(k)=k
<=> k2-3k-5=k
<=> k2-3k-5-k=0
<=> k2-4k-5=0
<=> k2-4k-4-1=0
<=> (k-2)2=1
<=> k-2=1 hoặc k-2=-1
<=> k=3 hoặc k=1


1/ B chia đa thức f(x) cho g(x) như bình thường, dư 3
Để chia hết, số dư phải bằng 0
hay x- 2 thuộc ước của 3 bằng \(\pm1,\pm3\)
Ta có bảng gt:
.....
Vậy..........

\(E=\left(2x-5\right)^{10}-12\ge-12\)
Dấu "=" xảy ra \(\Leftrightarrow x=\dfrac{5}{2}\)
Vậy \(E_{min}=-12\Leftrightarrow x=\dfrac{5}{2}\)
\(F=\left(x+5\right)^8+\left|x+5\right|+22\ge22\)
Dấu "=" xảy ra \(\Leftrightarrow x=-5\)
Vậy \(F_{min}=22\Leftrightarrow x=-5\)
\(G=17-\left|3x-2\right|\)
Dấu "=" xảy ra \(x=\dfrac{2}{3}\)
Vậy \(G_{max}=17\Leftrightarrow x=\dfrac{2}{3}\)
\(K=17-\left|3x-2\right|-\left(2-3x\right)^{2020}\le17\)
Dấu "=" xảy ra \(\Leftrightarrow x=\dfrac{2}{3}\)
Vậy \(K_{max}=17\Leftrightarrow x=\dfrac{2}{3}\)
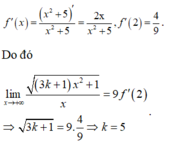
Ta có: \(x=x^2-3x-5\)
\(\Leftrightarrow x-x^2+3x=-5\)
\(\Leftrightarrow-x^2+4x=-5\)
\(\Rightarrow x=5\)Vậy \(k=5\)
hay do