Tìm n \(\inℤ^+\) bé nhất để
F = n3 + 4n2 - 20n - 48 ⋮ 125
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



b) Ta tính tổng các chữ số của số khi được tạo thành.
Xét các số có 1 chữ số thì tổng bằng \(45\).
Xét các số có 2 chữ số: tổng các chữ số hàng chục là \(10.1+...+10.9=10.45\)
tổng các chữ số hàng đơn vị là \(\left(0+1+2+...+9\right).9=9.45\)
Xét số có 3 chữ số thì tổng các chữ số là \(1+0+0=1\)
Do đó tổng các chữ số của số được tạo thành là \(45+10.45+9.45+1⋮̸9\)
Mà \(2016⋮9\)nên số tạo thành không chia hết cho \(2016\).

\(P=n^3+4n^2-20n-48=\left(n+2\right)\left(n-4\right)\left(n+6\right)\)
Với \(n=4\Rightarrow P=0⋮125\)(thỏa)
Với \(n< 4\)thử từng giá trị đều không thỏa.
Vậy số \(n\)nhỏ nhất cần tìm là \(4\).
\(n^3+4n^2-20n-48\)
\(=n^3-4n^2+8n^2-32n+12n-48\)
\(=\left(n^3-4n^2\right)+\left(8n^2-32n\right)+\left(12n-48\right)\)
\(=n^2\left(n-4\right)+8n\left(n-4\right)+12\left(n-4\right)\)
\(=\left(n-4\right)\left(n^2+8n+12\right)\)
Nhận thấy n = 4 thì biểu thức trên bằng 0, chia hết cho 125.
Vậy số tự nhiên n nhỏ nhất là bằng 4 (thử với n = 1, 2, 3 đều không chia hết cho 125)

Lời giải:
$125=5^3$
$A=n^3+7n^2+6n=n(n^2+7n+6)=n(n+1)(n+6)$
Nếu $n=5k$ với $k$ nguyên thì $n+1,n+6$ đều không chia hết cho $5$.
Do đó để $A\vdots $ thì $n\vdots 125$
Nếu $n=5k+1$ thì $n,n+1,n+6$ đều không chia hết cho $5$ nên $A\not\vdots 5$
Nếu $n=5k+2, 5k+3$ thì tương tự $n=5k+1$, loại
Nếu $n=5k+4$ thì $A=(5k+4)(5k+5)(5k+10)=25(5k+4)(k+1)(k+2)$
Để $A\vdots 125$ thì $(k+1)(k+2)\vdots 5$. Khi đó, $k+1\vdots 5$ hoặc $k+2\vdots 5$, hay $k$ có dạng $5t-1$ hoặc $5t-2$ với $t$ nguyên
$\Rightarrow n=5k+4=5(5t-1)+4=25t-1$ hoặc $n=5(5t-2)+4=25t-6$ với $t$ nguyên
Vậy $n$ có dạng $125t, 25t-1, 25t-6$ với $t$ là số nguyên nào đó.

F=(n+6)(n+2)(n−4)
n=5k+1 thì không thỏa mãn
n=5k+2 thì không thỏa mãn
n=5k+3 thì muốn 125|F thì k+1⋮25 rồi xét ....
Tương tự với 5k+4,5k

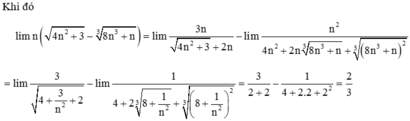
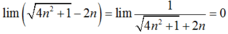
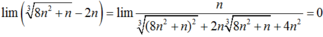
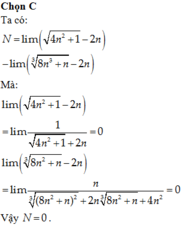
Ta có \(F=\left(n-4\right)\left(n+2\right)\left(n+6\right)\)
Với \(n=4;n=-2;n=-6\) thì hiển nhiên F chia hết cho 125. Nhưng do n là số nguyên dương nên ta chỉ chọn \(n=4\)
Nếu F khác 0:
Do F chia hết cho 125 nên F cũng chia hết cho 5. Do 5 là số nguyên tố nên 1 trong 3 số \(n-4,n+2,n+6\) sẽ phải chia hết cho 5.
Nếu số đó là \(n-4\) thì đương nhiên \(n+6=n-4+10⋮5\) và \(n+2=n-4+6⋮̸5\). Vậy F không chia hết cho 125.
Nếu số đó là \(n+6\) thì \(n-4=n+6-10⋮5\) và \(n+2=n+6-4⋮̸5\). Vậy F không chia hết cho 125.
Nếu số đó là \(n+2\) thì \(n-4=n+2-6⋮̸5\) và \(n-4=n+2-6⋮̸5\). Vậy F cũng không chia hết cho 125.
Như vậy số nguyên dương n nhỏ nhất thỏa mãn F chia hết cho 125 là \(n=4\)