Cho tam giác ABC vuông cân tại A. Gọi O là trung điểm của BC. Trên cạnh AB lấy M, trên cạnh AC lấy điểm N sao cho AM=CN. Xác định vị trí của M trên AB để khoảng cách từ O đến MN đạt nhỏ nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 8 2015
Bạn chỉ cần chứng minh AEDM là HCN ;O là trung điểm của DE =>O cũng là trung điểm của AM =>O,M,A thẳng hàng
b,
Gọi P ,Q lần lượt là trung điểm của AB,AC
=> giới hạn :
*Khi M trùng với B=> O trùng với P
*Khi M trùng với C=> O trùng với Q
=> I thuộc PQ
c,
Kẻ đường cao AH
Khi M trùng với H thì AM ngắn nhất (quan hệ đường vuông góc và đường xiên)
CM
27 tháng 10 2018
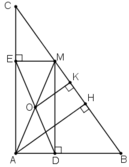
a) Tứ giác ADME có: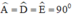 
⇒ ADME là hình chữ nhật
O là trung điiểm của đường chéo DE nên O cũng là trung điểm của đường chéo AM.
Vậy A, O, M thẳng hàng.
b) Kẻ AH ⊥ BC; OK ⊥ BC.
Ta có OA = OM, OK // AH (cùng vuông góc BC)
⇒ MK = KH
⇒ OK là đường trung bình của ΔMAH
⇒ OK = AH/2.
⇒ điểm O cách BC một khoảng cố định bằng AH/2
⇒ O nằm trên đường thẳng song song với BC.
Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB.
Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC.
c) Vì AH là đường cao hạ từ A đến BC nên AM ≥ AH (trong tam giác vuông thì cạnh huyền là cạnh lớn nhất).
Vậy AM nhỏ nhất khi M trùng H.
7 tháng 8 2018
cảm ơn bạn rất nhiều nhờ có bài toán này mà tôi đã nghĩ ra bài toán khác
chúc bạn học tốt
8 tháng 4 2015
a.xét tam giác BAN và tam giác CAM ta có:
AM=AN (GT)
AB=AC ( tam giác ABC cân tại A)
A là góc chung
suy ra tam giác BÀN= tam giác CẤM (c.g.c)
b. xét tam giác OBM và tam giác OCN ta có:
góc OBM=góc OCN (2 góc tương ứng)
BM=CN (AB=AC mà AM=AN)
Góc OMB= góc ONC (góc ANB= góc AMC mà AMC+OMB=ANB+ONC)
suy ra tam giác OMB= ta giác ONC (g.c.g)
c.xét tam giác AMO và tam giác ANO ta có:
AM=AN(GT)
góc AMO= góc ANO ( tam giác AMC= tam giác ANB)
OM=ON (tam giác MOB= tam giác NOC)
suy ra tam giác AMO=tam giác ANO (c.g.c)
suy ra góc BAO= góc CAO (2 góc tương ứng). suy ra Ao là p/g của góc A
gọi giao điểm của BC và AO là I.
Xét tam giác ABI và tam giác ACI ta có:
AB=AC (tam giác ABC cân tại A)
góc BAI= góc CAI (CMT)
AI là cạnh chung
suy ra tam giác ABI= tam giác ACI( c.g.c)
suy ra góc AIB= góc AIC (2 góc tương ứng) mà AIB+AIC= 180 độ nên AIB=AIC=180/2=90 độ suy ra AI vuông góc vs Bc. suy ra AO là đường cao của tam giác ABC.
d. khi M,N lần lượt là trung điểm của AB và AC thì BM=MN=NC.
BB
6 tháng 7 2017
a.xét tam giác BAN và tam giác CAM ta có:
AM=AN (GT)
AB=AC ( tam giác ABC cân tại A)
A là góc chung
suy ra tam giác BÀN= tam giác CẤM (c.g.c)
b. xét tam giác OBM và tam giác OCN ta có:
góc OBM=góc OCN (2 góc tương ứng)
BM=CN (AB=AC mà AM=AN)
Góc OMB= góc ONC (góc ANB= góc AMC mà AMC+OMB=ANB+ONC)
suy ra tam giác OMB= ta giác ONC (g.c.g)
c.xét tam giác AMO và tam giác ANO ta có:
AM=AN(GT)
góc AMO= góc ANO ( tam giác AMC= tam giác ANB)
OM=ON (tam giác MOB= tam giác NOC)
suy ra tam giác AMO=tam giác ANO (c.g.c)
suy ra góc BAO= góc CAO (2 góc tương ứng). suy ra Ao là p/g của góc A
gọi giao điểm của BC và AO là I.
Xét tam giác ABI và tam giác ACI ta có:
AB=AC (tam giác ABC cân tại A)
góc BAI= góc CAI (CMT)
AI là cạnh chung
suy ra tam giác ABI= tam giác ACI( c.g.c)
suy ra góc AIB= góc AIC (2 góc tương ứng) mà AIB+AIC= 180 độ nên AIB=AIC=180/2=90 độ suy ra AI vuông góc vs Bc. suy ra AO là đường cao của tam giác ABC.
d. khi M,N lần lượt là trung điểm của AB và AC thì BM=MN=NC.