Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E.
a,Tính số đo các cung BD,DE và EC
b,Gọi M và N lần lượt là điểm chính giữa các cung nhỏ BD và CE. So sánh các cung nhỏ BE, CD và MN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 3 2021
a) Gọi O là trung điểm của BC.
Ta có \(\stackrel\frown{BD}=\stackrel\frown{DE}=\stackrel\frown{EC}\Rightarrow\widehat{BOD}=\widehat{DOE}=\widehat{EOC}=60^o\).
Từ đó CE // AB, BD // AC.
Suy ra \(\Delta ABN\sim\Delta ECN\).
b) Theo tính đối xứng ta có BM = CN.
Ta có \(\dfrac{BN}{NC}=\dfrac{AB}{CE}=\dfrac{AB}{CO}=2\Rightarrow BN=2NC\Rightarrow MN=NC\).
Dễ dàng suy ra đpcm.
NH
13 tháng 1 2019
nối BE , CD
=> \(\widehat{BEC}=90,\widehat{CDB}=90\)
MÀ \(\widehat{ACB}=\widehat{ABC}=60\)
=>\(\widehat{CBE}=\widehat{BCD}=90-60=30\)
=> CUNG CE = CUNG BD
VÌ TAM GIÁC ĐỀU => CE VỪA LÀ ĐƯỜNG CAO CŨNG LÀ PHÂN GIÁC => CUNG BD = CUNG DE
CM
1 tháng 7 2019
4) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O) . Chứng minh ba điểm D, E, K thẳng hàng.
Vì N là điểm chính giữa cung nhỏ BC nên DN là trung trực của BC nên DN là phân giác B D C ^
Ta có K Q C ^ = 2 K M C ^ (góc nọi tiếp bằng nửa góc ở tâm trong dường tròn (Q))
N D C ^ = K M C ^ (góc nội tiếp cùng chắn cung N C ⏜ )
Mà B D C ^ = 2 N D C ^ ⇒ K Q C ^ = B D C ^
Xét 2 tam giác BDC & KQC là các các tam giác vuông tại D và Q có hai góc ở ⇒ B C D ^ = B C Q ^ do vậy D, Q, C thẳng hàng nên KQ//PK
Chứng minh tương tự ta có ta có D, P, B thẳng hàng và DQ//PK
Do đó tứ giác PDQK là hình bình hành nên E là trung điểm của PQ cũng là trung điểm của DK. Vậy D, E, K thẳng hàng (điều phải chứng minh).
3 tháng 12 2021
a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại H
Do đó: AH⊥BC
ML
5 tháng 5 2018
c.
Tứ giác IKNC là tứ giác nội tiếp (cmt)=> \(\widehat{IKC}=\widehat{INC}\)(cùng = \(\frac{1}{2}sđ\widebat{IC}\))
Xét đt(O) có: \(\widehat{ABC}=\widehat{ANC=}\widehat{INC}\)(cùng = \(\frac{1}{2}sđ\widebat{NC}\))
=> \(\widehat{ABC}=\widehat{IKC}\)mà 2 góc này ở vị trí đồng vị => IK // HB (dhnb)
Chứng minh tương tự câu a ta có: Tứ giác AMHI là tứ giác nội tiếp => \(\widehat{AHI}=\widehat{AMI}=\widehat{AMC}\)(cùng = \(\frac{1}{2}sđ\widebat{AI}\))
Xét đt(O) có: \(\widehat{ABC}=\widehat{AMC}\left(=\frac{1}{2}sđ\widebat{AC}\right)\)=> \(\widehat{ABC}=\widehat{AHI}\)mà 2 góc này ở vị trí đồng vị => HI // BK
Vì M là điểm chính giữa cung nhỏ \(\widebat{AB}\)(gt) => \(sđ\widebat{AM}=sđ\widebat{BM}\)
Xét đt(O) có: \(\widehat{ACM}=\frac{1}{2}sđ\widebat{AM}\)và \(\widehat{BCM}=\frac{1}{2}sđ\widebat{BM}\)=> \(\widehat{ACM}=\widehat{BCM}\)=> CM là tia phân giác của \(\widehat{ACB}\)
CMTT ta có: AN là tia phân giác của \(\widehat{BAC}\)
Mà 2 dây AN và CM cắt nhau tại I (gt) => BI là tia phân giác của \(\widehat{ABC}\)hay BI là tia phân giác của \(\widehat{HBK}\)
Xét tứ giác BHIK có:
* HI // BK (cmt)
* IK // HB (cmt)
=> tứ giác BHIK là hình bình hành (DHNB)
Mà BI là phân giác của \(\widehat{HBK}\)(cmt) => tứ giác BHIK là hình thoi (dhnb hình thoi)
d. Vì \(\widehat{NBK}=\widehat{BMN}=\widehat{BMK}\left(cmt\right)\)=> BN là tiếp tuyến tại B của đt (P) ngoại tiếp \(\Delta MBK\)=> \(BN\perp BP\)Mà \(BN\perp BD\)do \(\widehat{DBN}=90^o\)(góc nội tiếp chắn nửa đt) => B, P , D thẳng hàng
Tương tự ta có: C, Q, D thẳng hàng
\(\Delta BPK\)và \(\Delta DBC\)là 2 tam giác cân có chung góc ở đáy => góc ở đỉnh của chúng bằng nhau => \(\widehat{BPK}=\widehat{BDC}\)Mà 2 góc này ở vị trí đồng vị => PK // DC (dhnb) => PK // DQ
CMTT ta có: DP // QK => DPKQ là hình bình hành (dhnb HBH) => DK đi qua trung điểm của PQ => D, E, K thẳng hàng (đpcm)
ML
5 tháng 5 2018
a. Vì M là điểm chính giữa cung nhỏ \(\widebat{AB}\)(gt) => \(sđ\widebat{AM}=sđ\widebat{MB}\)=> \(\widehat{ACM}=\widehat{BCM}\)(2 góc nội tiếp chắn 2 cung = nhau)
Lại có: \(\widehat{ACM}=\widehat{ANM}\)(CÙNG = \(\frac{1}{2}sđ\widebat{AM}\)) => \(\widehat{MNA}=\widehat{BCM}\)hay \(\widehat{KNI}=\widehat{KCI}\)(Do M,K,N và A,I,N => \(\widehat{MNA}=\widehat{KNI}\); M,I,C và B,K,C => \(\widehat{BCM}=\widehat{KCI}\)) => IKNC là tứ giác nội tiếp (Dấu hiệu nhận biết)
b. Xét đường tròn (O) có: \(\widehat{BMN}=\frac{1}{2}sđ\widebat{BN}\)và \(\widehat{NBC}=\widehat{NBK}=\frac{1}{2}sđ\widebat{NC}\)
mà N là điểm chính giữa cung nhỏ \(\widebat{BC}\)(gt) => sđ \(\widebat{BN}\)= sđ \(\widebat{NC}\)=> \(\widehat{BMN}=\widehat{NBK}\)
Xét \(\Delta BMN\)và \(\Delta KBN\)có:
* \(\widehat{N}\)chung
* \(\widehat{BMN}=\widehat{NBK}\)(cmt)
=> \(\Delta BMN~\Delta KBN\)(g.g) => \(\frac{NB}{NK}=\frac{NM}{NB}\)<=> \(NB^2=NK.NM\)(đpcm)
CM
13 tháng 5 2018
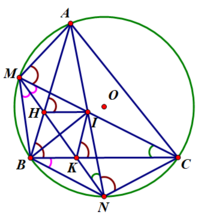
2) Chứng minh N B 2 = N K . N M .
Ta có N là điểm chính giữa cung B C ⏜ ⇒ B N ⏜ = C N ⏜ ⇒ B M N ^ = C M N ^ (góc nội tiếp chắn 2 cung bằng nhau)
Mà C B N ^ = C M N ^ (góc nội tiếp chắn cùng chắn cung C N ⏜ )
C B N ^ = B M N ^ (cùng bằng góc C M N ^ ) ⇒ K B N ^ = B M N ^
Xét Δ K B N v à Δ B M N có:
N ^ chung
K B N ^ = B M N ^
⇒ Δ K B N ∽ Δ B M N ⇒ K N B N = B N M N ⇒ N B 2 = N K . N M
(điều phải chứng minh).
CM
23 tháng 8 2018
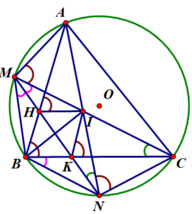
3) Chứng minh tứ giác BHIK là hình thoi.
Ta có A B C ^ = A N C ^ (góc nội tiếp cùng chắn cung A C ⏜ )
Mà A M C ^ = A H I ^ (góc nội tiếp cùng chắn cung I C ⏜ )
⇒ A B C ^ = I K C ^ Mà 2 góc này ở vị trí đồng vị nên H B / / I K (1)
+ Chứng minh tương tự phần 1 ta có tứ giác AMHI nội tiếp
A N C ^ = I K C ^ (góc nội tiếp cùng chắn cung A I ⏜ )
Ta có A B C ^ = A M C ^ (góc nội tiếp cùng chắn cung A C ⏜ )
⇒ A B C ^ = A H I ^ Mà 2 góc này ở vị trí đồng vị nên B K / / H I (2)
Từ (1) và (2) suy ra tứ giác BHIK là hình bình hành.
Mặt khác AN, CM lần lượt là các tia phân giác của các góc A và C trong tam giác ABC nên I là giao điêm 3 đường phân giác, do đó BI là tia phân giác góc B
Vậy tứ giác BHIK là hình thoi (dấu hiệu nhận biết hình thoi).