Một người đi xe máy chuyển động theo 3 giai đoạn: Giai đoạn 1: người đó đi trên đoạn đường đầu dài 3,2km với vận tốc V1 = 16km/h. Giai đoạn 2: người đó chuyển động với vận tốc trung bình V2 = 15km/h trong 30 phút. Giai đoạn 3: chuyển động đều trên quãng đường 4km trong thời gian 10 phút. Tính vận tốc trung bình trên cả 3 quãng đường.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(t_1=\frac{S_1}{v_1}=\frac{1}{6}\)
\(S_2=v_2.t_2=10km\)
\(S=S_1+S_2+S_3=16km\)
\(t=t_1+t_2+t_3=\frac{5}{6}h\)
\(\Rightarrow v_{tb}=\frac{S}{t}=19,2\) km/h

Giải:
Thời gian xe máy chuyển động giai đoạn đầu t 1 = S 1 v 1 = 10 30 = 1 3 h
Quãng đường giai đoạn hai chuyển động S 2 = v 2 t 2 = 40. 1 2 = 20 k m
Tổng quãng đường và thời gian vật chuyển động
S = S 1 + S 2 + S 3 = 10 + 20 + 4 = 34 k m
t = t 1 + t 2 + t 3 = 1 3 + 1 2 + 1 6 = 1 h
⇒ v t b = S t = 34 1 = 34 k m / h

Thời gian xe máy chuyển động giai đoạn đầu
![]()
Quãng đường giai đoạn hai chuyển động
![]()
Tổng quãng đường và thời gian vật chuyển động
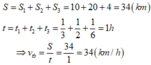

t1=S1v1=16t1=S1v1=16
S2=v2.t2=10kmS2=v2.t2=10km
S=S1+S2+S3=16kmS=S1+S2+S3=16km
t=t1+t2+t3=56ht=t1+t2+t3=56h
⇒vtb=St=19,2⇒vtb=St=19,2 km/h

đổi: 45p=0,75h
8250m=8,25km
15p=0,25h
thời gian người đó đi hết quãng đường 1 là
\(t_1=\dfrac{S_1}{V_1}=\dfrac{5}{20}=0,25\left(h\right)\)
quãng đường 2 dài là
S2=V2.t2=25.0,75=18,75(km)
vận tốc trung bình của xe trên cả 3 giai đoạn là
\(V_{tb}=\dfrac{S_1+S_2+S_3}{t_1+t_2+t_3}=\dfrac{5+18,75+8,25}{0,25+0,75+0,25}=25,6\left(km/h\right)\)

t1=S1v1=16t1=S1v1=16
S2=v2.t2=10kmS2=v2.t2=10km
S=S1+S2+S3=16kmS=S1+S2+S3=16km
t=t1+t2+t3=56ht=t1+t2+t3=56h
⇒vtb=St=19,2⇒vtb=St=19,2 km/h

Thời gian người đó đi hết đoạn đường 1 là: \(t_1=\dfrac{s_1}{v_1}=\dfrac{3,2}{16}=0,2\left(h\right)\)
Quãng đường người đó đi được ở đoạn đường 2 là: \(s_2=v_2t_2=15.\dfrac{30}{60}=7,5\left(km\right)\)
Vận tốc trung bình trên cả 3 quãng đường:
\(v_{tb}=\dfrac{s}{t}=\dfrac{3,2+7,5+4}{0,2+\dfrac{30}{60}+\dfrac{10}{60}}\approx17\left(\dfrac{km}{h}\right)\)