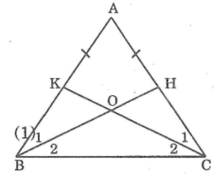
Cho tam giác ABC cân tại A . Lấy điiểm M thuộc cạnh AB , điểm N thuộc cạnh AC sao cho BM=CN . gọi O là giao điểm của BN và CM . chứng minh rằng ;
a)tam giac AMN cân từ đó suy ra MN // BC
b) tam giác BOM = tam giác CNO
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{BAM}\) chung
AM=AN
Do đó: ΔABM=ΔACN
Suy ra: BM=CN
b: Xét ΔNBC và ΔMCB có
NB=MC
NC=MB
BC chung
Do đó: ΔNBC=ΔMCB
Suy ra: \(\widehat{GNB}=\widehat{GMC}\)
Xét ΔGNB và ΔGMC có
\(\widehat{GNB}=\widehat{GMC}\)
NB=MC
\(\widehat{GBN}=\widehat{GCM}\)
Do đó: ΔGNB=ΔGMC

a) +Xét tam giác ABC cân tại A có \(\widehat{A}\)= 100o
=>\(\widehat{B}=\widehat{C}=40^o\)
TT ta có: Tam giác AMN cân(AM=AN) tại A có\(\widehat{A}\)=100o
=>\(\widehat{AMN}=\widehat{ANM}=40^o\)
=>\(\widehat{B}=\widehat{C}\)\(=\widehat{AMN}=\widehat{ANM}\)
=>\(\widehat{B}=\widehat{AMN}\)
Mà hai góc này đồng vị =>MN//BC
+Xét tam giác AMC và tam giác ANB có:
AM=AN
 chung
AC=AB
Do đó tam giác AMC= tam giác ANB(c.g.c)
Suy ra BN=CM(hai cạnh t.ứ)
Bài 2 để tí mik lm tiếp, mik đag bận, bạn tích mik để mik có cái để tl tiếp nhé
Chúc học tốt

a: AM+MC=AC
NA+NB=AB
mà AB=AC; AM=AN
nên MC=NB
b: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
BC chung
=>ΔNBC=ΔMCB
=>góc OBC=góc OCB
=>ΔOBC cân tại O

Bài làm
a) Ta có: AM = MB = AB
AN +NC = AC
Mà AM = AN ( gt ), AB = AC ( ∆ABC cân )
=> BM = CN .
b) Xét tam giác ABN và tam giác ACM có:
AB = AC ( ∆ABC cân )
^A chung
AM = AN ( gt )
=> ∆ABN = ∆ACM ( c.g.c )
c) Vì ∆ABN = ∆ACM ( cmt )
=> ^ABN = ^ACM ( hai góc tương ứng ).
=> ^AMC = ^ANB
Ta có: ^AMC + ^BMC = 180°. ( Kề bù )
^ANB + ^BNC = 180° ( kề bù )
Mà ^AMC = ^ANB ( cmt )
=> ^BMC = ^CNB
Xét tam giác MIB và tam giác NIC có:
^BMC = ^CNB ( cmt )
BM = NC ( cmt )
^ABN = ^ACM ( cmt )
=> ∆MIB = ∆NIC ( g.c.g )
=> BI = IC ( hai cạnh tương ứng )
=> ∆BIC cân tại I

Bài làm
a) Xét tam giác AMN có:
AM = AN
=> Tam giác AMN cân tại A.
b) Xét tam giác ABC cân tại A có:
\(\widehat{B}=\frac{180^0-\widehat{A}}{2}\) (1)
Xét tam giác AMN cân tại A có:
\(\widehat{M}=\frac{180^0-\widehat{A}}{2}\) (2)
Từ (1) và (2) => \(\widehat{B}=\widehat{M}\)
Mà hai góc này ở vị trí đồng vị.
=> MN // BC
c) Xét tam giác ABN và tam giác ACM có:
AN = AM ( gt )
\(\widehat{A}\) chung
AB = AC ( Vì tam giác ABC cân )
=> Tam giác ABN = tam giác ACM ( c.g.c )
=> \(\widehat{ABN}=\widehat{ACM}\)( hai cạnh tương ứng )
Ta có: \(\widehat{ABN}+\widehat{MBC}=\widehat{ABC}\)
\(\widehat{ACM}+\widehat{MCB}=\widehat{ACB}\)
Mà \(\widehat{ABN}=\widehat{ACM}\)( cmt )
\(\widehat{ABC}=\widehat{ACB}\)( hai góc kề đáy của tam giác cân )
=> \(\widehat{IBC}=\widehat{ICB}\)
=> Tam giác BIC cân tại I
Vì MN // BC
=> \(\widehat{MNI}=\widehat{IBC}\)( so le trong )
\(\widehat{NMI}=\widehat{ICB}\)( so le trong )
Và \(\widehat{IBC}=\widehat{ICB}\)( cmt )
=> \(\widehat{MNI}=\widehat{NMI}\)
=> Tam giác MIN cân tại I
d) Xét tam giác cân AMN có:
E là trung điểm của MN
=> AE là trung tuyến
=> AE là đường trung trực.
=> \(\widehat{AEN}=90^0\) (1)
Xét tam giác cân MNI có:
E là trung điểm MN
=> IE là đường trung tuyến
=> IE là trung trực.
=> \(\widehat{IEN}=90^0\) (2)
Cộng (1) và (2) ta được:\(\widehat{IEN}+\widehat{AEN}=90^0+90^0=180^0\) => A,E,I thẳng hàng. (3)
Xét tam giác cân BIC có:
F là trung điểm BC
=> IF là trung tuyến
=> IF là trung trực.
=> \(\widehat{IFC}=90^0\)
Và MN // BC
Mà \(\widehat{IFC}=90^0\)
=> \(\widehat{IEN}=90^0\)
=> E,I,F thẳng hàng. (4)
Từ (3) và (4) => A,E,I,F thẳng hàng. ( đpcm )
# Học tốt #

a.xét tam giác BAN và tam giác CAM ta có:
AM=AN (GT)
AB=AC ( tam giác ABC cân tại A)
A là góc chung
suy ra tam giác BÀN= tam giác CẤM (c.g.c)
b. xét tam giác OBM và tam giác OCN ta có:
góc OBM=góc OCN (2 góc tương ứng)
BM=CN (AB=AC mà AM=AN)
Góc OMB= góc ONC (góc ANB= góc AMC mà AMC+OMB=ANB+ONC)
suy ra tam giác OMB= ta giác ONC (g.c.g)
c.xét tam giác AMO và tam giác ANO ta có:
AM=AN(GT)
góc AMO= góc ANO ( tam giác AMC= tam giác ANB)
OM=ON (tam giác MOB= tam giác NOC)
suy ra tam giác AMO=tam giác ANO (c.g.c)
suy ra góc BAO= góc CAO (2 góc tương ứng). suy ra Ao là p/g của góc A
gọi giao điểm của BC và AO là I.
Xét tam giác ABI và tam giác ACI ta có:
AB=AC (tam giác ABC cân tại A)
góc BAI= góc CAI (CMT)
AI là cạnh chung
suy ra tam giác ABI= tam giác ACI( c.g.c)
suy ra góc AIB= góc AIC (2 góc tương ứng) mà AIB+AIC= 180 độ nên AIB=AIC=180/2=90 độ suy ra AI vuông góc vs Bc. suy ra AO là đường cao của tam giác ABC.
d. khi M,N lần lượt là trung điểm của AB và AC thì BM=MN=NC.
a.xét tam giác BAN và tam giác CAM ta có:
AM=AN (GT)
AB=AC ( tam giác ABC cân tại A)
A là góc chung
suy ra tam giác BÀN= tam giác CẤM (c.g.c)
b. xét tam giác OBM và tam giác OCN ta có:
góc OBM=góc OCN (2 góc tương ứng)
BM=CN (AB=AC mà AM=AN)
Góc OMB= góc ONC (góc ANB= góc AMC mà AMC+OMB=ANB+ONC)
suy ra tam giác OMB= ta giác ONC (g.c.g)
c.xét tam giác AMO và tam giác ANO ta có:
AM=AN(GT)
góc AMO= góc ANO ( tam giác AMC= tam giác ANB)
OM=ON (tam giác MOB= tam giác NOC)
suy ra tam giác AMO=tam giác ANO (c.g.c)
suy ra góc BAO= góc CAO (2 góc tương ứng). suy ra Ao là p/g của góc A
gọi giao điểm của BC và AO là I.
Xét tam giác ABI và tam giác ACI ta có:
AB=AC (tam giác ABC cân tại A)
góc BAI= góc CAI (CMT)
AI là cạnh chung
suy ra tam giác ABI= tam giác ACI( c.g.c)
suy ra góc AIB= góc AIC (2 góc tương ứng) mà AIB+AIC= 180 độ nên AIB=AIC=180/2=90 độ suy ra AI vuông góc vs Bc. suy ra AO là đường cao của tam giác ABC.
d. khi M,N lần lượt là trung điểm của AB và AC thì BM=MN=NC.

+) Xét ΔABH và ΔACK, ta có:
AB = AC ( vì tam giác ABC cân tại A)
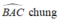
AH = AK (giả thiết)
Suy ra: ΔABH = ΔACK(c.g.c)

+ Do đó, tam giác OBC cân tại O.