Diện tích hình bình hành 24cm2. Khoảng cách từ giao điểm 2 đường chéo đến các cạnh của hình bình hành bằng 2cm và 3cm. Tính chu vi hình bình hành
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: AB/DC ( tứ giác ABCD là HBH) => góc ABO = góc CDO ( 2 góc slt)
Ta có: BC//AD ( tứ giác ABCD là HBH) => góc CBO = góc ADO ( 2 góc slt)
Ta có: tứ giác ABCD là HBH => giao điểm O là trung điểm của AC và BD
Xét tam giác AEO và tam giác CFO có:
Góc BAO = góc DCO ( cmt)
OA = OC ( O trung điểm của AC )
góc EOA = góc FOC ( đối đỉnh)
=> tam giác AEO = giác CFO ( c.g.c)
=> EO = FO ( 2 cạnh tương ứng) => O là trung điểm của EF
Xét tam giác BHO = tam giác DGO có:
góc CBO = góc ADO (cmt)
OD = OB ( O là trung điểm của DB )
Góc GOD = góc HOB ( đối đỉnh)
=> tam giác BHO = DGO ( g.c.g)
=> HO = GO ( 2 cạnh tương ứng) => O là trung điểm của GH
Xét tứ giác EGFH
ta có: GH cắt EF tại O
Mà O là trung điểm của EF (cmt)
O là trung điểm của GH (cmt)
=> Tứ giác EGFH là hình bình hành.

GIẢI:
Nối hai điểm AC ta được 2 hình tam giác ACN và ACM có diện tích bằng nhau (vì có độ dài đáy bằng nhau AM = CN = 14 cm và chiều cao bằng nhau AD = BC = 18 cm).
Diện tích hình tam giác ACN là:
14 x 8 : 2 = 56 (cm2)
Ta có: Diện tích hình bình hành AMCN = diện tích hình tam giác ACN = diện tích hình tam giác ACM.
Diện tích hình bình hành AMCN là:
56 x 2 = 112 (cm2)
Đáp số: 112 cm2.
(tick giúp với ạ)

Đáp án B
Gọi hình bình hành là ABCD và
d:x+ y-1 = 0, ∆: 3x – y+ 5= 0 .
Không làm mất tính tổng quát giả sử
![]()
Ta có : ![]() . Vì I(3;3) là tâm hình bình hành nên C(7;4) ;
. Vì I(3;3) là tâm hình bình hành nên C(7;4) ; ![]()
=> Đường thẳng ACcó pt là: x- 4y + 9= 0.
Do ![]() => Đường thẳng BC đi qua điểm C và có vtpt
=> Đường thẳng BC đi qua điểm C và có vtpt ![]() có pt là: 3x – y- 17= 0.
có pt là: 3x – y- 17= 0.
Khi đó :
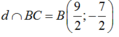
Ta có:
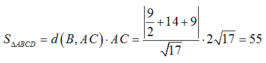

Diện tích bình hành:
24 x 12= 288(cm2)
Độ dày cạnh đáy của hình bình hành đó là:
288:16=18(cm2)