Hai phương trình có vô số nghiệm chưa chắc đã tương đương, có ai cho mình đc ví dụ không?? mình đang cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 9 2018
- Bạn Nga đã nhận xét đúng vì hai hệ phương trình cùng vô nghiệm có nghĩa là chúng cùng có tập nghiệm bằng ∅.
- Bạn Phương nhận xét sai.
Ví dụ: Xét hai hệ 
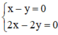và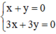 
Hệ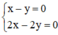 
có vô số nghiệm. Tập nghiệm của (I) được biểu diễn bởi đường thẳng x – y = 0.
Hệ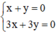 
có vô số nghiệm. Tập nghiệm của (II) được biểu diễn bởi đường thẳng x + y = 0.
Nhận thấy, tập nghiệm của hai hệ (I) và hệ (II) được biểu diễn bởi hai đường thẳng khác nhau nên hai hệ không tương đương.
CM
8 tháng 2 2017
- Bạn Nga đã nhận xét đúng vì hai hệ phương trình cùng vô nghiệm có nghĩa là chúng cùng có tập nghiệm bằng ∅.
- Bạn Phương nhận xét sai.
Ví dụ: Xét hai hệ 
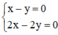và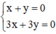 
Hệ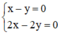 
có vô số nghiệm. Tập nghiệm của (I) được biểu diễn bởi đường thẳng x – y = 0.
Hệ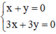 
có vô số nghiệm. Tập nghiệm của (II) được biểu diễn bởi đường thẳng x + y = 0.
Nhận thấy, tập nghiệm của hai hệ (I) và hệ (II) được biểu diễn bởi hai đường thẳng khác nhau nên hai hệ không tương đương.
Kiến thức áp dụng
Hai hệ phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.
CM
3 tháng 4 2019
a) Hệ đã cho vô nghiệm bởi vì mỗi nghiệm của hệ là nghiệm chung của hai phương trình, một phương trình vô nghiệm thì hệ không có nghiệm chung.
b) Hệ đã cho có vô số nghiệm.
PT
1
CM
16 tháng 2 2018
Hai bất phương trình trong VD 1 không tương đương do chúng không có cùng tập nghiệm.
CM
30 tháng 4 2018
Ví dụ: phương trình (1) x - 1 = 3 có tập nghiệm S1 = {4}.
Nhân hai vế của phương trình (1) với x, ta được phương trình:
(x - 1)x = 3x (2)
⇔ (x - 1)x - 3x = 0
⇔ x(x - 4) = 0
Phương trình (2) có tập nghiệm là S2 = {0, 4}.
Vì S1 ≠ S2 nên hai phương trình (1) và (2) không tương đương.
CM
27 tháng 3 2019
Hệ đã cho vô nghiệm bởi vì mỗi nghiệm của hệ là nghiệm chung của hai phương trình, một phương trình vô nghiệm thì hệ không có nghiệm chung.
17 tháng 1 2022
a) \(\left\{{}\begin{matrix}mx+y=1.\\x+my=m+1.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1-mx.\\x+m\left(1-mx\right)=m+1.\left(1\right)\end{matrix}\right.\)
Xét (1): \(x+m\left(1-mx\right)=m+1.\Leftrightarrow x+m-m^2x-m-1=0.\Leftrightarrow\left(1-m^2\right)x-1=0.\left(2\right)\)
Để hệ phương trình có nghiệm duy nhất. \(\Leftrightarrow\) (2) có nghiệm duy nhất.
\(\Leftrightarrow1-m^2\ne0.\Leftrightarrow m^2\ne1.\Leftrightarrow m\ne\pm1.\)
b) Để hệ phương trình có vô số nghiệm. \(\Leftrightarrow\) (2) có vô số nghiệm.
\(\Leftrightarrow\left\{{}\begin{matrix}1-m^2=0.\\-1=0.\end{matrix}\right.\) (vô lý).
\(\Rightarrow m\in\phi\).
c) Để hệ phương trình có vô nghiệm. \(\Leftrightarrow\) (2) có vô nghiệm.
\(\Leftrightarrow\left\{{}\begin{matrix}1-m^2=0.\\-1\ne0.\end{matrix}\right.\)\(\Leftrightarrow1-m^2=0.\Leftrightarrow m^2=1.\Leftrightarrow m=\pm1.\)
pt trên thì có nghiệm là 2/3;
pt dưới có chuyễn hóa thành:
9x^2-6x=0
có thêm nghiệm nữa bằng 0;
cho thêm ví dụ nữa nè:
có thằng phân tích -20=-20 ra (5-9/2)^2=(4-9/2)^2
thực chất kết quả của nó là 0,1^2=(-0,1)^2
k mk nhé thanks bạn nhìu nhìu
k mk nhé mk nhanh nhất