1. hai công nhân được giao làm cùng 1 loại sản phẩm với số lượng và thời gian như nhau. Người thứ nhất mỗi giờ làm tăng 1 sản phẩm nên đã hoàn thành trước công việc 2 giờ. Người thứ 2 mỗi giờ làm tăng 2 sản phẩm, nên chẳng những đã hoàn thành công việc trước thời hạn 3 giờ mà còn vượt mức 7 sản phẩm nữa. Tính số lượng sản phẩm mà mỗi người được giao làm.
2. a, Một người mua 30 con chim gồm 3 loại : chim sẻ, chim ngói và chim bồ câu hết tất cả 30 đồng. Biết 3 con chim sẻ giá 1 đồng, 2 con chim ngói giá 1 đồng và mỗi con bồ câu giá 2 đồng. Hỏi mỗi loại có mấy con.
b,Một con ngựa giá 204 Đô. Có 3 người mua ngựa nhưng mỗi người đều không đủ tiền mua. Người thứ nhất nói với 2 người kia: mỗi người cho tôi vay nửa số tiền của mình thì tôi đủ tiền mua ngựa. Người thứ hai nói với 2 người kia: mỗi người cho tôi vay \(\frac{1}{3}\)số tiền của mình , tôi sẽ mua được ngựa. Người thứ 3 nói : chỉ cần các anh cho tôi vay \(\frac{1}{4}\)số tiền của mình thì con ngựa sẽ là của tôi. Hãy cho biết mỗi người có bao nhiêu tiền ?
CÁC BẠN ƠI, GIẢI CHI TIẾT GIÚP MÌNH VỚI, MÌNH ĐANG CẦN GẤP. CẢM ƠN CÁC BẠN NHIỀU ^=^

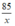 (giờ)
(giờ) (giờ)
(giờ)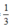 giờ nên ta có phương trình
giờ nên ta có phương trình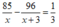
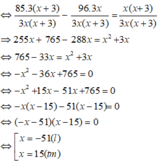
1/ Gọi năng suất, thời gian, số sản phẩm 2 người được giao là: x (sản phầm/h) , y (h), z (sản phẩm)
Người thứ nhất làm với năng suất: x + 1 nên ta có
\(\left(x+1\right)\left(y-2\right)=z\left(1\right)\)
Người thứ 2 làm với năng suất: x + 2 nên ta có
\(\left(x+2\right)\left(y-3\right)-7=z\left(2\right)\)
Năng suất đự định làm là: x nên ta có
\(xy=z\left(3\right)\)
Từ (1), (2), (3) ta có hệ: \(\hept{\begin{cases}\left(x+1\right)\left(y-2\right)=z\\\left(x+2\right)\left(y-3\right)-7=z\\xy=z\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=9\\y=20\\z=180\end{cases}}\)
2/ a/ Gọi số chim sẻ chim ngói và bồ câu mua là: x, y, z (con)
Giá 1 con chim sẻ là: \(\frac{1}{3}\)đồng
Giá 1 con chim ngói: \(\frac{1}{2}\)đồng
Giá 1 con chim bồ câu: 2 đồng
Ta có tổng số chim là 30 nên: x + y + z = 30
Tổng số tiền mua là 30 nên: \(\frac{x}{3}+\frac{y}{2}+2z=30\)
Từ đây ta có hệ: \(\hept{\begin{cases}x+y+z=30\\\frac{x}{3}+\frac{y}{2}+2z=30\end{cases}\Leftrightarrow}\hept{\begin{cases}x+y+z=30\\2x+3y+12z=180\end{cases}}\)
\(\hept{\begin{cases}x+y+z=30\left(1\right)\\y+10z=120\left(2\right)\end{cases}}\)
Xét (2) ta có: \(y+10z=120\)
\(y=120-10z\)
Mà \(1\le y\le30\)
\(\Rightarrow1\le120-10z\le30\Leftrightarrow9\le z\le11\)
Thế vô tìm được \(\left(x,y,z\right)=\left(0,20,10;9,10,11\right)\)